Zeroth order logic

☞ This page belongs to resource collections on Logic and Inquiry.

Zeroth order logic is an informal term that is sometimes used to indicate the common principles underlying the algebra of sets, boolean algebra, boolean functions, logical connectives, monadic predicate calculus, propositional calculus, and sentential logic. The term serves to mark a level of abstraction in which the more inessential differences among these subjects can be subsumed under the appropriate isomorphisms.

Propositional forms on two variables

By way of initial orientation, Table 1 lists equivalent expressions for the sixteen functions of concrete type 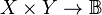$X \times Y \to \mathbb{B}\!$ and abstract type 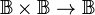$\mathbb{B} \times \mathbb{B} \to \mathbb{B}\!$ in a number of different languages for zeroth order logic.

$\text{Table 1.} ~~ \text{Propositional Forms on Two Variables}\!$
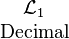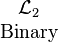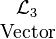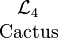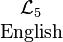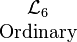$\begin{matrix}\mathcal{L}_1 \\ \text{Decimal}\end{matrix}\!$	$\begin{matrix}\mathcal{L}_2 \\ \text{Binary}\end{matrix}\!$	$\begin{matrix}\mathcal{L}_3 \\ \text{Vector}\end{matrix}\!$	$\begin{matrix}\mathcal{L}_4 \\ \text{Cactus}\end{matrix}\!$	$\begin{matrix}\mathcal{L}_5 \\ \text{English}\end{matrix}\!$	$\begin{matrix}\mathcal{L}_6 \\ \text{Ordinary}\end{matrix}\!$
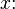	$x\colon\!$	$1~1~0~0\!$
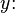	$y\colon\!$	$1~0~1~0\!$
$\begin{matrix} f_{0} \\[4pt] f_{1} \\[4pt] f_{2} \\[4pt] f_{3} \\[4pt] f_{4} \\[4pt] f_{5} \\[4pt] f_{6} \\[4pt] f_{7} \end{matrix}\!$	$\begin{matrix} f_{0000} \\[4pt] f_{0001} \\[4pt] f_{0010} \\[4pt] f_{0011} \\[4pt] f_{0100} \\[4pt] f_{0101} \\[4pt] f_{0110} \\[4pt] f_{0111} \end{matrix}\!$	$\begin{matrix} 0~0~0~0 \\[4pt] 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~0~1~1 \\[4pt] 0~1~0~0 \\[4pt] 0~1~0~1 \\[4pt] 0~1~1~0 \\[4pt] 0~1~1~1 \end{matrix}\!$	$\begin{matrix} \texttt{(~)} \\[4pt] \texttt{(} x \texttt{)(} y \texttt{)} \\[4pt] \texttt{(} x \texttt{)} ~ y ~ \\[4pt] \texttt{(} x \texttt{)} \\[4pt] ~ x ~ \texttt{(} y \texttt{)} \\[4pt] \texttt{(} y \texttt{)} \\[4pt] \texttt{(} x \texttt{,} ~ y \texttt{)} \\[4pt] \texttt{(} x ~ y \texttt{)} \end{matrix}\!$	$\begin{matrix} \text{false} \\[4pt] \text{neither}~ x ~\text{nor}~ y \\[4pt] y ~\text{without}~ x \\[4pt] \text{not}~ x \\[4pt] x ~\text{without}~ y \\[4pt] \text{not}~ y \\[4pt] x ~\text{not equal to}~ y \\[4pt] \text{not both}~ x ~\text{and}~ y \end{matrix}\!$	$\begin{matrix} 0 \\[4pt] \lnot x \land \lnot y \\[4pt] \lnot x \land y \\[4pt] \lnot x \\[4pt] x \land \lnot y \\[4pt] \lnot y \\[4pt] x \ne y \\[4pt] \lnot x \lor \lnot y \end{matrix}\!$
$\begin{matrix} f_{8} \\[4pt] f_{9} \\[4pt] f_{10} \\[4pt] f_{11} \\[4pt] f_{12} \\[4pt] f_{13} \\[4pt] f_{14} \\[4pt] f_{15} \end{matrix}\!$	$\begin{matrix} f_{1000} \\[4pt] f_{1001} \\[4pt] f_{1010} \\[4pt] f_{1011} \\[4pt] f_{1100} \\[4pt] f_{1101} \\[4pt] f_{1110} \\[4pt] f_{1111} \end{matrix}\!$	$\begin{matrix} 1~0~0~0 \\[4pt] 1~0~0~1 \\[4pt] 1~0~1~0 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~0 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \\[4pt] 1~1~1~1 \end{matrix}\!$	$\begin{matrix} x ~ y \\[4pt] \texttt{((} x \texttt{,} ~ y \texttt{))} \\[4pt] y \\[4pt] \texttt{(} x ~ \texttt{(} y \texttt{))} \\[4pt] x \\[4pt] \texttt{((} x \texttt{)} ~ y \texttt{)} \\[4pt] \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] \texttt{((~))} \end{matrix}\!$	$\begin{matrix} x ~\text{and}~ y \\[4pt] x ~\text{equal to}~ y \\[4pt] y \\[4pt] \text{not}~ x ~\text{without}~ y \\[4pt] x \\[4pt] \text{not}~ y ~\text{without}~ x \\[4pt] x ~\text{or}~ y \\[4pt] \text{true} \end{matrix}\!$	$\begin{matrix} x \land y \\[4pt] x = y \\[4pt] y \\[4pt] x \Rightarrow y \\[4pt] x \\[4pt] x \Leftarrow y \\[4pt] x \lor y \\[4pt] 1 \end{matrix}\!$

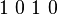These six languages for the sixteen boolean functions are conveniently described in the following order:

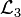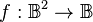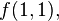
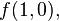
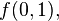
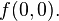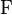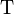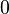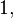Language $\mathcal{L}_{3}\!$ describes each boolean function $f : \mathbb{B}^2 \to \mathbb{B}\!$ by means of the sequence of four boolean values, $f(1,1),\!$ $f(1,0),\!$ $f(0,1),\!$ $f(0,0).\!$ Such a sequence, perhaps in another order, and perhaps with the logical values $\mathrm{F}\!$ and $\mathrm{T}\!$ instead of the boolean values $0\!$ and $1,\!$ respectively, would normally be displayed as a column in a truth table.

Language 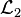$\mathcal{L}_{2}\!$ lists the sixteen functions in the form 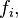$f_i,\!$ where the index 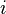$i\!$ is a bit string formed from the sequence of boolean values in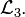 $\mathcal{L}_{3}.\!$

Language 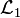$\mathcal{L}_{1}\!$ notates the boolean functions 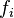$f_i\!$ with an index 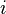$i\!$ that is the decimal equivalent of the binary numeral index in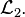 $\mathcal{L}_{2}.\!$

Language 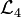$\mathcal{L}_{4}\!$ expresses the sixteen functions in terms of logical conjunction, indicated by concatenating function names or proposition expressions in the manner of products, plus the family of minimal negation operators, the first few of which are given in the following variant notations:

$\begin{matrix} \texttt{()} & = & 0 & = & \mathrm{false} \\[6pt] \texttt{(} x \texttt{)} & = & \tilde{x} & = & x^\prime \\[6pt] \texttt{(} x \texttt{,} y \texttt{)} & = & \tilde{x}y \lor x\tilde{y} & = & x^\prime y \lor x y^\prime \\[6pt] \texttt{(} x \texttt{,} y \texttt{,} z \texttt{)} & = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} & = & x^\prime y z \lor x y^\prime z \lor x y z^\prime \end{matrix}\!$

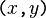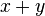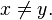It may be noted that $\texttt{(} x \texttt{,} y \texttt{)}\!$ is the same function as $x + y\!$ and $x \ne y.$ The inclusive disjunctions indicated for 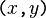$\texttt{(} x \texttt{,} y \texttt{)}\!$ and for 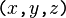$\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}\!$ may be replaced with exclusive disjunctions without affecting the meaning, since the terms disjoined are already disjoint. However, the function 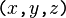$\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}\!$ is not the same thing as the function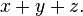 $x + y + z.\!$

Language 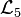$\mathcal{L}_{5}\!$ lists ordinary language expressions for the sixteen functions. Many other paraphrases are possible, but these afford a sample of the simplest equivalents.

Language 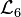$\mathcal{L}_{6}\!$ expresses the sixteen functions in one of several notations that are commonly used in formal logic.

Translations

中文 : 零阶逻辑

Syllabus

Focal nodes

Peer nodes

Logical operators

Relational concepts

Information, Inquiry

Document history

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

This article is issued from Wikiversity - version of the Monday, November 09, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.