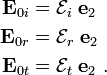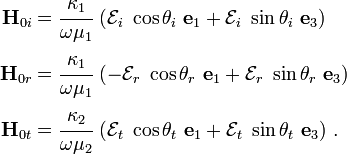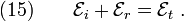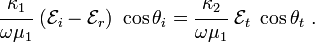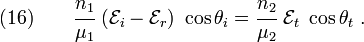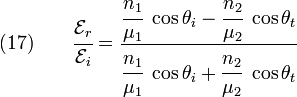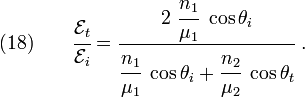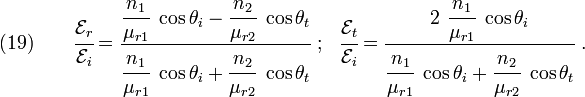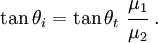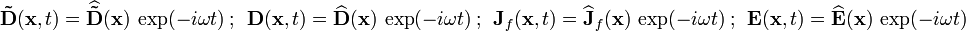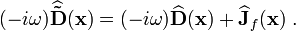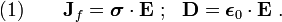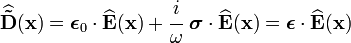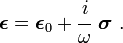Waves in composites and metamaterials/Fresnel equations
< Waves in composites and metamaterialsThe content of these notes is based on the lectures by Prof. Graeme W. Milton (University of Utah) given in a course on metamaterials in Spring 2007.
A brief excursion into homogenization
One of the first questions that arise in the homogenization of composites is whether determining the effective behavior of the composite by some averaging process is the right thing to do. At this stage we ignore such questions and assume that there is a representative volume element (RVE) over which such an average can be obtained.
Let 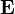 be an average over some RVE of the
be an average over some RVE of the 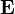 -field at an atomic
scale. Similarly, let
-field at an atomic
scale. Similarly, let 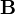 be the average of the
be the average of the 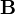 -field.
Recall, from the previous lecture, that the Maxwell equations have the form
(we have dropped the hats over the field quantities)
-field.
Recall, from the previous lecture, that the Maxwell equations have the form
(we have dropped the hats over the field quantities)
For some conductors, at low frequencies, the permittivity tensor is given by
where 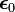 is the real part of the permittivity tensor and
is the real part of the permittivity tensor and 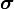 is the electrical conductivity tensor.
[1]
is the electrical conductivity tensor.
[1]
A mixture of conductors and dielectric materials may have properties which are quite different from those of the constituents. For example, consider the checkerboard material shown in Figure 1 containing an isotropic conducting material and an isotropic dielectric material.
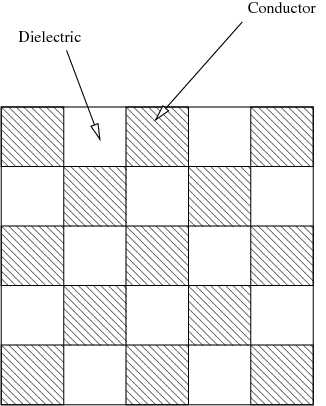 Figure 1. Checkerboard material containing conducting and dielectric phases. |
The conducting material has a permittivity of 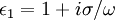 while the dielectric material has a permittivity of
while the dielectric material has a permittivity of 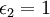 . The
effective permittivity of the checkerboard is given by
. The
effective permittivity of the checkerboard is given by
Plane waves
Let us assume that the material is isotropic. Then,
Therefore, we can write
The Maxwell equations then take the form
If we assume that  and
and  do not depend upon position, i.e.,
do not depend upon position, i.e.,
 and
and 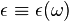 , and
take the curl of equations (2), we get
, and
take the curl of equations (2), we get
Using the identity 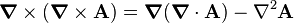 ,
we get
,
we get
Since
we have
Therefore, from equation (3), we have
We can also write the above equations in the form
where  is the phase velocity (the velocity at which the wave crests
travel). To have a propagating wave,
is the phase velocity (the velocity at which the wave crests
travel). To have a propagating wave,  must be real. This will be the
case when
must be real. This will be the
case when  and
and 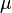 are both positive or both negative (see
Figure 2).
are both positive or both negative (see
Figure 2).
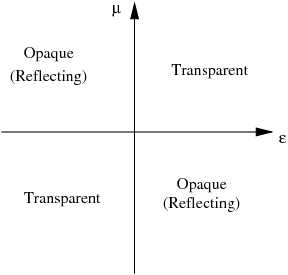 Figure 2. Transparency and opacity of a material as a function of 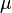 and and  . . |
Let us look for plane wave solutions to the equations (4) of the form
where 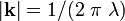 and
and 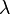 is the wavelength. Then,
using the first of equations (2) we have
is the wavelength. Then,
using the first of equations (2) we have
where 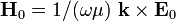 .
.
Since 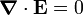 , we have (in terms of components with
respect to a orthonormal Cartesian basis)
, we have (in terms of components with
respect to a orthonormal Cartesian basis)
Hence,
Similarly, since 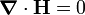 , we have
, we have
Hence,
Plugging equation (5) into the first of equations (4) we get
Reverting back to Gibbs notation, we get
Therefore,
Plugging the solution (6) into the second of equations (4) (and using index notation as before) we get
In Gibbs notation, we then have
Therefore, once again, we get
Reflection at an Interface
The following is based on the description given in [Lorrain88]. Figure 3 shows an electromagnetic wave that is incident upon an interface separating two mediums.
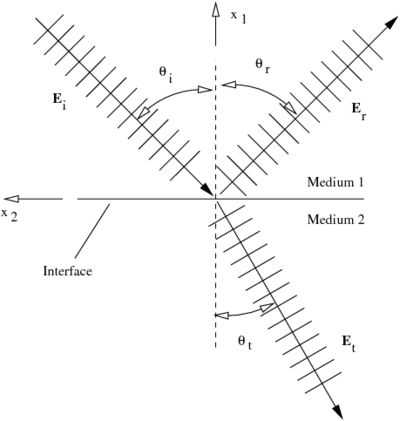 Figure 3. Reflection of an electromagnetic wave at an interface. |
We ignore the time-dependent component of the electric fields and assume that we can express the waves shown in Figure 3 in the form
where 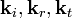 are the wave vectors.
are the wave vectors.
Since the oscillations at the interface must have the same period (the requirement of continuity), we must have
This means that the tangential components of 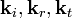 must
be equal at the interface. Therefore,
must
be equal at the interface. Therefore,
Now,
where 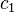 and
and 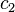 are the phase velocities in medium 1 and medium 2,
respectively. Hence we have,
are the phase velocities in medium 1 and medium 2,
respectively. Hence we have,
This implies that
The refractive index is defined as
where 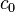 is the phase velocity is vacuum. Therefore, we get
is the phase velocity is vacuum. Therefore, we get
Polarized wave with the 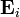 parallel to the plane of incidence
parallel to the plane of incidence
Consider the 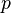 -polarized wave shown in Figure 4. The
figure represents an infinite wave polarized with the
-polarized wave shown in Figure 4. The
figure represents an infinite wave polarized with the 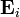 vector
polarized parallel to the plane of incidence. This is also called the
TM (transverse magnetic) case.
vector
polarized parallel to the plane of incidence. This is also called the
TM (transverse magnetic) case.
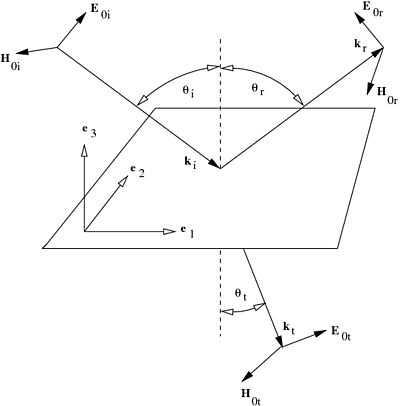 Figure 4. Infinite wave polarized with the 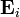 -vector parallel to the plane of incidence. -vector parallel to the plane of incidence. |
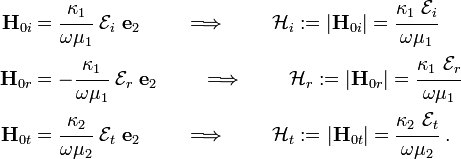
Let us define
Recall that,
Let us choose an orthonormal basis (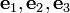 ) such that
the
) such that
the 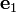 vector lies on the interface and is parallel the plane of
incidence. The
vector lies on the interface and is parallel the plane of
incidence. The 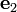 vector lies on the plane of incidence and the
vector lies on the plane of incidence and the
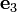 vector is normal to the interface. Then the vectors
vector is normal to the interface. Then the vectors 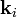 ,
,
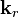 , and
, and 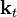 may be expressed in this basis as
may be expressed in this basis as
Similarly, defining
we get
Using the definition
we then get
Hence, with the vector 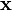 expressed as
expressed as
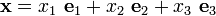 , we get
, we get
Similarly,
At the interface, continuity requires that the tangential components of
the vectors 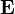 and
and 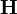 are continuous. Clearly, from the above
equations, the
are continuous. Clearly, from the above
equations, the 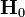 vectors are tangential to the interface. Also,
at the interface
vectors are tangential to the interface. Also,
at the interface 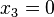 and
and  is arbitrary. Hence, continuity
of the components of
is arbitrary. Hence, continuity
of the components of 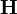 at the interface can be achieved if
at the interface can be achieved if
In terms of the electric field, we then have
Recall that the refractive index is given by 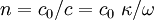 .
Therefore, we can write the above equation as
.
Therefore, we can write the above equation as
The tangential components of the 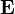 vectors at the interface are given
by
vectors at the interface are given
by 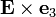 . Therefore, the tangential components of the
. Therefore, the tangential components of the
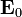 vectors at the interface are
vectors at the interface are
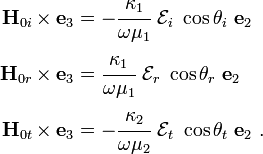
Using the arbitrariness of  and from the continuity of the
and from the continuity of the 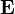 vectors at the interface, we have
vectors at the interface, we have
Since 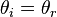 , we have
, we have
From equations (7) and (8), we get two more relations:
and
Equations (7), (8), (9),
and (10) are the Fresnel equations for 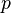 -polarized
electromagnetic waves.
-polarized
electromagnetic waves.
If we define,
where 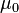 is the permeability of vacuum, then we can write equations
(9) and (10) as
is the permeability of vacuum, then we can write equations
(9) and (10) as
Note that
For non-magnetic materials we have 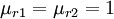 . Hence,
. Hence,
Also, from Snell's law
Combining equations (12) and (13), we get
If 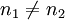 we have
we have 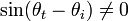 . Hence,
. Hence,
This is the condition that defines Brewster's angle
(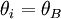 ). Plugging
equation (14) into equation (13), we get
). Plugging
equation (14) into equation (13), we get
This relation can be used to solve for Brewster's angle for various media. At Brewster's angle, we have
Hence, the sign of 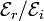 changes at the Brewster angle.
changes at the Brewster angle.
Also, note that if 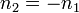 and
and 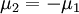 , since
, since
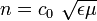 we must have
we must have 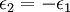 . Then,
by Snell's law
. Then,
by Snell's law
Hence,
So the radiation is transmitted at the angle 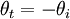 and
none is reflected.
and
none is reflected.
More can be said about the matter. In fact, an interface separating media
with 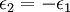 and
and 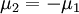 "behaves like a
mirror". Consider the interface in Figure 5. Suppose that
on the left side of the mirror,
"behaves like a
mirror". Consider the interface in Figure 5. Suppose that
on the left side of the mirror, 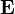 and
and 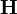 solve Maxwell's
equations
solve Maxwell's
equations
Let the solution be of the form
Suppose that the right hand side of the interface has reflected fields, i.e.,
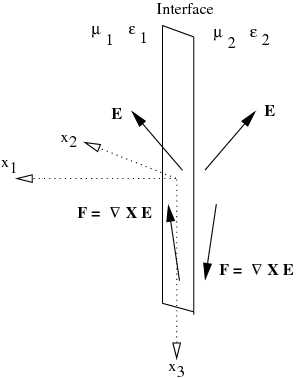 Figure 5. Reflection at an interface due to negative  and and 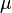 . . |
Also, on the right hand side, let
Then, to the right of the interface, we have
or,
Polarized wave with the 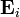 perpendicular to the plane of incidence
perpendicular to the plane of incidence
For a plane polarized wave with the 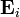 vector perpendicular to the
plane of incidence, we have
vector perpendicular to the
plane of incidence, we have
Therefore,
Continuity of tangential components of 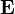 at the interface gives
at the interface gives
The tangential components of 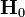 at the interface are given by
at the interface are given by
From continuity at the interface and using the arbitrariness of  , we
get (from the above equations with
, we
get (from the above equations with 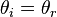 )
)
Using the relation 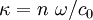 , we get
, we get
From equations (15) and (16), we get
and
Equations (15), (16), (17), and (18) are the Fresnel equations a wave polarized with the 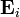 vector perpendicular to the plane of incidence. We may also
write the last two equations as
vector perpendicular to the plane of incidence. We may also
write the last two equations as
From the above equations, there is no reflected wave only if
This is only possible if there is no interface. Therefore, in the presence of a interface, there is always a reflected wave for this situation.
Footnotes
- ↑ The above relation for the permittivity tensor can be obtained as follows.
Recall that
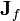 and the electric displacement
and the electric displacement
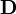 are related to the electric field
are related to the electric field 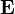 by
by
References
[Lorrain88]
P. Lorrain, D. R. Corson, and F. Lorrain. Electromagnetic fields and waves: including electric circuits. Freeman, New York, 1988.
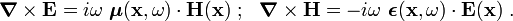
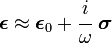
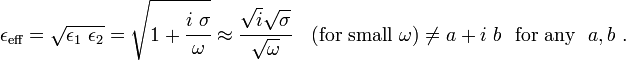
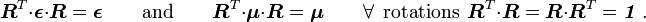
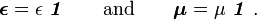
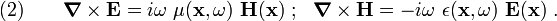
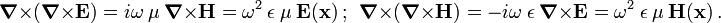
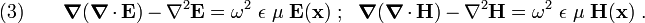
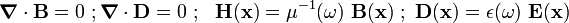
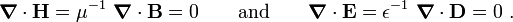
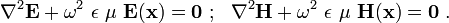
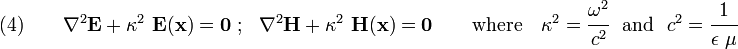
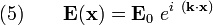
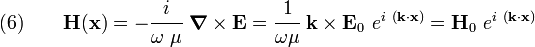
![\boldsymbol{\nabla} \cdot \mathbf{E} = \frac{\partial }{\partial x_m}\left[ E_{0m}~e^{i(k_l~x_l)}\right]
= i~k_l~\frac{\partial x_l}{\partial x_m}~E_{0m}~e^{i(k_l~x_l)}
= i~k_m~E_{0m}~e^{i(k_l~x_l)}
= i~(\mathbf{k}\cdot\mathbf{E}_0)~e^{i(\mathbf{k}\cdot\mathbf{x})} = 0 ~.](../I/m/bb3bf99fa22442f6275317581c254cc1.png)
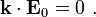
![\boldsymbol{\nabla} \cdot \mathbf{H} = \cfrac{1}{\omega\mu}\left[
\frac{\partial }{\partial x_m}\left(\mathcal{E}_{mpq}~k_p~E_{0q}~e^{i(k_l~x_l)}\right)
\right]
= \cfrac{i}{\omega\mu}\left[\mathcal{E}_{mpq}~k_p~E_{0q}~k_m~e^{i(k_l~x_l)}
\right]
= \cfrac{i}{\omega\mu}~\mathbf{k}\cdot(\mathbf{k}\times\mathbf{E}_0)~e^{i(\mathbf{k}\cdot\mathbf{x})}~.](../I/m/44d6f1be880607073dec4e75a1820d30.png)
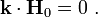
![\begin{align}
\left[\nabla^2 \mathbf{E} + \kappa^2~\mathbf{E}(\mathbf{x})\right]_n & =
\frac{\partial }{\partial x_m}\left[\frac{\partial }{\partial x_m}\left(
E_{0n}~e^{i k_l x_l}\right)\right] + \kappa^2~E_{0n}~
e^{i k_l x_l} \\
& =
\frac{\partial }{\partial x_m}\left[E_{0n}~\left(i~k_l~\frac{\partial x_l}{\partial x_m}\right)~
e^{i k_l x_l}\right] + \kappa^2~E_{0n}~
e^{i k_l x_l} \\
& =
i~E_{0n}~k_m~\frac{\partial }{\partial x_m}\left(e^{i k_l x_l}\right) +
\kappa^2~E_{0n}~
e^{i k_l x_l} \\
& =
i~E_{0n}~k_m~\left(i~k_l~\frac{\partial x_l}{\partial x_m}\right)~e^{i k_l x_l} +
\kappa^2~E_{0n}~
e^{i k_l x_l} \\
& =
- E_{0n}~k_m~k_m~e^{i k_l x_l} +
\kappa^2~E_{0n}~e^{i k_l x_l} ~.
\end{align}](../I/m/a7a13c4329854ebe60a93761960e0145.png)
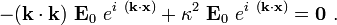
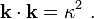
![\begin{align}
\left[\nabla^2 \mathbf{H} + \kappa^2~\mathbf{H}(\mathbf{x})\right]_n & =
\cfrac{1}{\omega\mu}\left\{
\frac{\partial }{\partial x_m}\left[\frac{\partial }{\partial x_m}\left(
\mathcal{E}_{npq}~k_p~E_{0q}~e^{i k_l x_l}\right)\right] + \kappa^2~
\mathcal{E}_{npq}~k_p~E_{0q}~e^{i k_l x_l}\right\} \\
& =
\cfrac{1}{\omega\mu}\left\{
\frac{\partial }{\partial x_m}
\left[\mathcal{E}_{npq}~k_p~E_{0q}~\left(i~k_l~\frac{\partial x_l}{\partial x_m}\right)~
e^{i k_l x_l}\right] + \kappa^2~
\mathcal{E}_{npq}~k_p~E_{0q}~e^{i k_l x_l}\right\} \\
& =
\cfrac{1}{\omega\mu}\left\{
i~\mathcal{E}_{npq}~k_p~k_m~E_{0q}~\left[i~k_l~\frac{\partial x_l}{\partial x_m}\right]~
e^{i k_l x_l} + \kappa^2~
\mathcal{E}_{npq}~k_p~E_{0q}~e^{i k_l x_l}\right\} \\
& =
\cfrac{1}{\omega\mu}\left\{
- \mathcal{E}_{npq}~k_p~k_m~k_m~E_{0q}~e^{i k_l x_l} + \kappa^2~
\mathcal{E}_{npq}~k_p~E_{0q}~e^{i k_l x_l}\right\}
\end{align}](../I/m/a793d0616b0f4f24bdbc06130a1552c6.png)
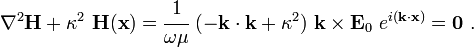
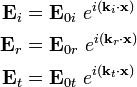

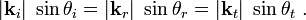
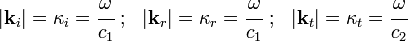
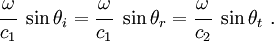
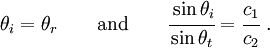
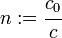
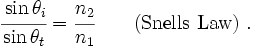
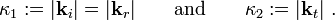
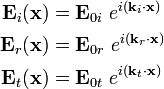
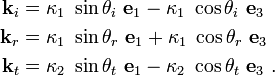
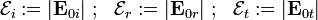
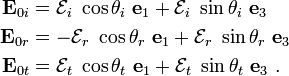
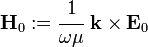
![\begin{align}
\mathbf{E}_i(\mathbf{x}) & =
(\mathcal{E}_i~\cos\theta_i~\mathbf{e}_1 + \mathcal{E}_i~\sin\theta_i~\mathbf{e}_3)
~e^{i[\kappa_1(x_1\sin\theta_i - x_3\cos\theta_i)]} \\
\mathbf{E}_r(\mathbf{x}) & =
(-\mathcal{E}_r~\cos\theta_r~\mathbf{e}_1 + \mathcal{E}_r~\sin\theta_r~\mathbf{e}_3)
~e^{i[\kappa_1(x_1\sin\theta_r + x_3\cos\theta_r)]} \\
\mathbf{E}_t(\mathbf{x}) & =
(\mathcal{E}_t~\cos\theta_t~\mathbf{e}_1 + \mathcal{E}_t~\sin\theta_t~\mathbf{e}_3)
~e^{i[\kappa_2(x_1\sin\theta_t - x_3\cos\theta_t)]}~.
\end{align}](../I/m/4d743a3b2d973c067c4dbb2ff9a5afaa.png)
![\begin{align}
\mathbf{H}_i(\mathbf{x}) & = -\mathcal{H}_i~\mathbf{e}_2~
~e^{i[\kappa_1(x_1\sin\theta_i - x_3\cos\theta_i)]} \\
\mathbf{H}_r(\mathbf{x}) & = -\mathcal{H}_r~\mathbf{e}_2~
~e^{i[\kappa_1(x_1\sin\theta_r + x_3\cos\theta_r)]} \\
\mathbf{H}_t(\mathbf{x}) & = -\mathcal{H}_t~\mathbf{e}_2~
~e^{i[\kappa_2(x_1\sin\theta_t - x_3\cos\theta_t)]}~.
\end{align}](../I/m/84342e42f4395629f6630d3bc0d6d808.png)
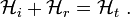
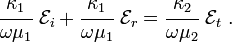
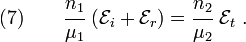
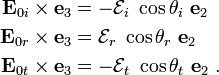
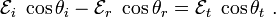
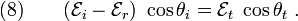
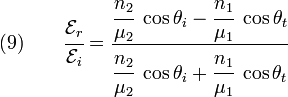
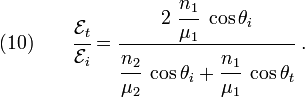
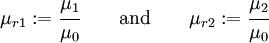
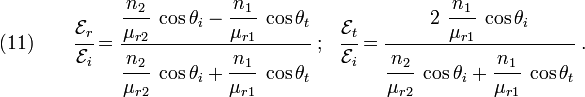
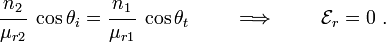
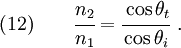
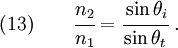
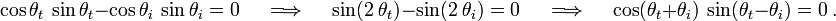
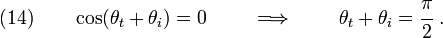
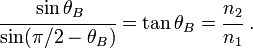
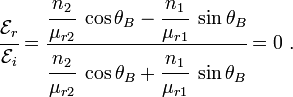
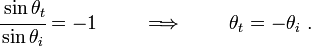
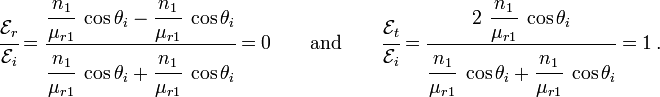
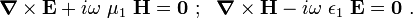
![\mathbf{E}(\mathbf{x}) = [E_1(\mathbf{x}), E_2(\mathbf{x}), E_3(\mathbf{x})] ~~\text{and}~~
\mathbf{H}(\mathbf{x}) = [H_1(\mathbf{x}), H_2(\mathbf{x}), H_3(\mathbf{x})] ~.](../I/m/27587347cc5ce9ae08caf83e22c71d2d.png)
![\begin{align}
\mathbf{E}(\mathbf{x}) & = [-E_1(-x_1,x_2,x_3), E_2(-x_1,x_2,x_3),
E_3(-x_1,x_2,x_3)] ~~\text{and}~~ \\
\mathbf{H}(\mathbf{x}) & = [-H_1(-x_1,x_2,x_3), H_2(-x_1,x_2,x_3),
H_3(-x_1,x_2,x_3)] ~.
\end{align}](../I/m/d199304f429e046862017ae3dcaa8525.png)
![\boldsymbol{\nabla} \times \mathbf{E} = [F_1(\mathbf{x}), F_2(\mathbf{x}), F_3(\mathbf{x})] ~.](../I/m/16a96a7b11016dcfb0e9d5d6d68231a9.png)
![\begin{align}
\boldsymbol{\nabla} \times \mathbf{E} = & \left\{
\left[\frac{\partial }{\partial x_2}[E_3(-x_1,x_2,x_3)] -
\frac{\partial }{\partial x_3}[E_2(-x_1,x_2,x_3)]\right],\right. \\
&
\left[-\frac{\partial }{\partial x_3}[E_1(-x_1,x_2,x_3)] +
\frac{\partial }{\partial x_1}[E_3(-x_1,x_2,x_3)]\right], \\
& \left.
\left[-\frac{\partial }{\partial x_1}[E_2(-x_1,x_2,x_3)] +
\frac{\partial }{\partial x_2}[E_1(-x_1,x_2,x_3)]\right]\right\}
\end{align}](../I/m/fb120c31286cba7afffd1de1b93e8a32.png)
![\boldsymbol{\nabla} \times \mathbf{E} = [F_1(-x_1,x_2,x_3), -F_2(-x_1,x_2,x_3), -F_3(x_1,x_2,x_3)]~.](../I/m/386eede79bf7c4ab32ea582f293c5569.png)