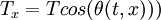Vibrating string

A string is stretched between two vertical bars that are a distance 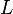$L$ apart as shown in the diagram below.

We will designate the vertical position of any point on the string at time "t" as 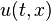$u(t,x)$ . Note that the vertical position depends on two variables, time and the horizontal position.

For this example each end is fixed thus the boundary conditions are 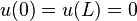$u(0) = u(L) =0$ and we are only interested in vertical motion of the string.

Now we are going to develop a partial differential equation that models the motion (dynamical behavior) of a point 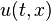$u(t,x)$ on the string when the string is initially displaced as shown in the figure above at time "t=0" and released. We will assume that the string is under a large tension and the vertical displacements are small.

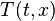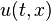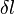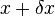Let $T(t,x)$ represent the tension in the string at point $u(t,x)$ . For a small length of string $\delta l$ with ends at $x$ and $x + \delta x$ , the tension at each end will be the same.

The tension on the left and right form angles with the horizontals as shown the figure below. The tension can now be expressed in terms of the components $T_{x} = T cos(\theta(t,x)))$

This article is issued from Wikiversity - version of the Wednesday, March 05, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.