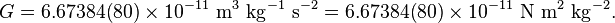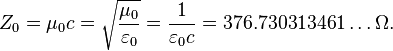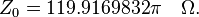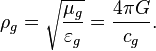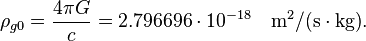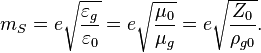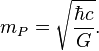Vacuum constants
Vacuum constants are physical constants associated with the fields existing in the free space under high vacuum. The values of these constants can be determined from the analysis of the interaction of fields with matter. Vacuum constants come in a variety of physical equations as necessary coefficients. Because of this, great importance is the refinement of these constants in special experiments.
Basic constants
Speed of light: [1] 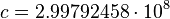 m/s, as exact value. It has become a defined constant in the SI system of units.
m/s, as exact value. It has become a defined constant in the SI system of units.
Vacuum permittivity: [2] 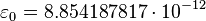 F/m.
F/m.
Speed of gravity 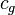 . It is supposed that
. It is supposed that 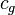 equals to the speed of light.
equals to the speed of light.
Derivative constants
Vacuum permeability: 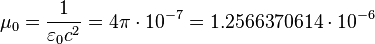 H/m in the SI system of units.
H/m in the SI system of units.
Electromagnetic impedance of free space:
Since 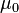 and
and  have exact values the same is for impedance of free space:
have exact values the same is for impedance of free space:
Gravitoelectric gravitational constant:
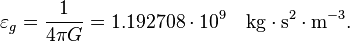
Gravitomagnetic gravitational constant:
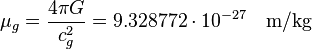 , if
, if 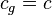 .
.
Gravitational characteristic impedance of free space:
If 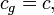 then gravitational characteristic impedance of free space equals to: [3] [4]
then gravitational characteristic impedance of free space equals to: [3] [4]
Constants  ,
, 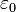 ,
, 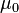 and
and 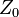 belong to selfconsistent electromagnetic constants, and constants
belong to selfconsistent electromagnetic constants, and constants 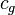 ,
, 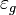 ,
, 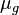 and
and 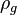 belong to selfconsistent gravitational constants.
belong to selfconsistent gravitational constants.
Vacuum constants are used for creation of natural units such as Stoney units and Planck units. For example, Stoney mass is connected with elementary charge  :
:
The Planck mass is connected with Dirac constant 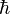 :
:
The Stoney length and the Stoney energy, collectively called the Stoney scale, are not far from the Planck length and the Planck energy, the Planck scale.
References
- ↑ CODATA value: Speed of Light in Vacuum. The NIST reference on Constants, Units, and Uncertainty. NIST.
- ↑ Latest (2010) values of the constants
- ↑ J. D. Kraus, IEEE Antennas and Propagation. Magazine 33, 21 (1991).
- ↑ Raymond Y. Chiao. "New directions for gravitational wave physics via “Millikan oil drops”, arXiv:gr-qc/0610146v16 (2007).PDF