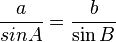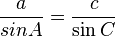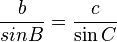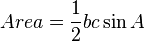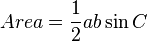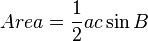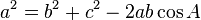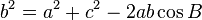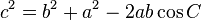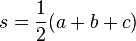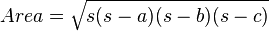Trigonometry/Plane

Plane trigonometry involves solving the mathematics of triangles. The law of sines and cosines are fundamental to this.

Law of sines

\frac {a}{sin A}=\frac{b}{\sin B}

\frac {a}{sin A}=\frac{c}{\sin C}

\frac {b}{sin B}=\frac{c}{\sin C}

Area of a triangle

Area=\frac{1}{2}bc \sin A

Area=\frac{1}{2}ab \sin C

Area=\frac{1}{2}ac \sin B

Law of cosines

This law uses the Pythagorean theorem, but this includes non-right angles.

a^2=b^2+c^2-2ab\cos A

b^2=a^2+c^2-2ab\cos B

c^2=b^2+a^2-2ab\cos C

Heron's area formula

s is the semi-perimeter

s=\frac{1}{2}(a+b+c)

Area=\sqrt{s(s-a)(s-b)(s-c)}

References

^[1] ^[2]

↑ Trigonometry (7th ed.), Addison Wesley, 2001, 0-321-05759-7
↑ "Trigonometry". Britannica 28: 619. (1993). University of Chicago. 0-85229-571-5. Retrieved on Jan 2, 2013.

This article is issued from Wikiversity - version of the Wednesday, January 02, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.