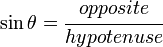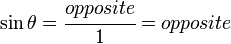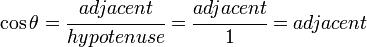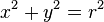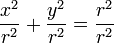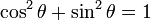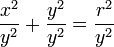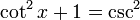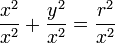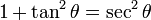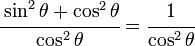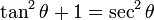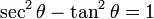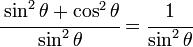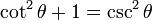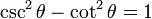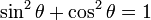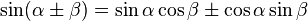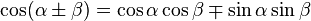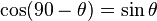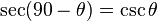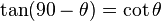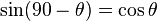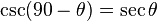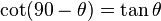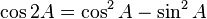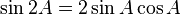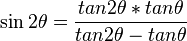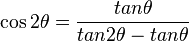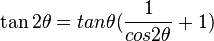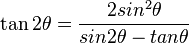Trigonometry/Identities

< Trigonometry

Let us take a right angled triangle with hypotenuse length 1. If we mark one of the acute angles as 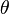\theta, then using the definition of the sine ratio, we have

\sin \theta = \cfrac{opposite}{hypotenuse}


As the hypotenuse is 1,

\sin \theta = \cfrac{opposite}{1} = opposite


Repeating the same process using the definition of the cosine ratio, we have

\cos \theta = \cfrac{adjacent}{hypotenuse} = \cfrac{adjacent}{1} = adjacent


Pythagorean identities

Since this is a right triangle, we can use the Pythagorean Theorem:

x^2 + y^2 = r^2

\frac{x^2}{r^2} + \frac{y^2}{r^2} = \frac{r^2}{r^2}

\operatorname{cos}^2 \theta + \operatorname{sin}^2 \theta = 1

This is the most fundamental identity in trigonometry.

\frac{x^2}{y^2} + \frac{y^2}{y^2} = \frac{r^2}{y^2}

\operatorname{cot}^2 x + 1 = \operatorname{csc}^2

\frac{x^2}{x^2} + \frac{y^2}{x^2} = \frac{r^2}{x^2}

\operatorname 1 + \operatorname{tan}^2\theta = \operatorname{sec}^2\theta

From this identity, if we divide through by squared cosine, we are left with:

\cfrac{\operatorname{sin}^2 \theta + \operatorname{cos}^2 \theta}{\operatorname{cos}^2 \theta} = \cfrac{1}{\operatorname{cos}^2 \theta}

\operatorname{tan}^2 \theta + 1 = \operatorname{sec}^2\theta

\operatorname{sec}^2 \theta - \operatorname{tan}^2 \theta = 1

If instead we divide the original identity by squared sine, we are left with:

\cfrac{\operatorname{sin}^2 \theta + \operatorname{cos}^2 \theta}{\operatorname{sin}^2 \theta} = \cfrac{1}{\operatorname{sin}^2 \theta}

\operatorname{cot}^2 \theta + 1 = \operatorname{csc}^2 \theta

\operatorname{csc}^2 \theta - \operatorname{cot}^2 \theta = 1

There are basically 3 main trigonometric identities. The proofs come directly from the definitions of these functions and the application of the Pythagorean theorem:

\operatorname{sin}^2 \theta + \operatorname{cos}^2 \theta = 1
\operatorname{sec}^2 \theta - \operatorname{tan}^2 \theta = 1
\operatorname{csc}^2 \theta - \operatorname{cot}^2 \theta = 1


Angle sum-difference identities

\sin(\alpha \pm \beta)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta
\cos(\alpha \pm \beta)=\cos \alpha\cos \beta\mp \sin \alpha \sin \beta

Cofunction identities

\cos(90-\theta)=\sin\theta
\sec(90-\theta)=\csc\theta
\tan(90-\theta)=\cot\theta
\sin(90-\theta)=\cos\theta
\csc(90-\theta)=\sec\theta
\cot(90-\theta)=\tan\theta

Multiple angle identities

\cos2A=\cos^2A-\sin^2A
\sin2A=2\sin A\cos A
\sin 2\theta= \frac{tan 2\theta*tan\theta}{tan 2\theta-tan\theta}
\cos 2\theta=\frac{tan \theta}{tan 2\theta - tan\theta}
\tan 2\theta=tan\theta(\frac{1}{cos 2\theta}+1)
\tan 2\theta=\frac{2sin^2\theta}{sin 2\theta-tan\theta}
This article is issued from Wikiversity - version of the Saturday, September 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.