Trigonometry/Functions

This resource emphasizes the right triangle and hence angles in the first quadrant: 0<θ<π/2
See also Trigonometry/Polar for an approach that is useful for ∞<θ<∞

There are six trigonometric functions in Trigonometry: sine, cosine, tangent, cotangent, secant, and cosecant. These define useful ratios of one side to another in a right triangle: given the angle, you know the sine; given the sine, you know the angle, etc.

The definitions of these functions refer to one of the acute angles of the right triangle.

If we use the Greek letter θ to identify this angle, then:

Sine

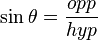
Sine θ is the length of the leg opposite θ over the length of the hypotenuse: $\sin\theta=\frac{opp}{hyp}$

Cosine

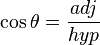
Cosine θ is the length of the leg adjacent to θ over the hypotenuse: $\cos\theta=\frac{adj}{hyp}$

Tangent

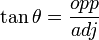
Tangent of θ is the length of the leg on the opposite side of the triangle from the angle θ over the length of the leg of the triangle adjacent to the angle θ: $\tan\theta=\frac{opp}{adj}$

These three can be memorized by use of the name of the princess "Soh Cah Toa," meaning:

"sine-opposite-hypotenuse
cosine-adjacent-hypotenuse
tangent-opposite-adjacent".

The remaining ratios are reciprocals of the previous ratios:

Cotangent

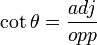
Cotangent θ is the reciprocal of tangent θ: $\cot\theta=\frac{adj}{opp}$

Secant

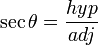
Secant θ is the reciprocal of cosine θ: $\sec\theta=\frac{hyp}{adj}$

Cosecant

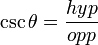
Cosecant θ is the reciprocal of sine θ: $\csc\theta=\frac{hyp}{opp}$

Other considerations

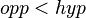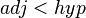
Since the hypotenuse of a right triangle is always the longest side, $opp < hyp\,$ and $adj < hyp\,$
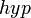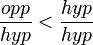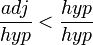
If we divide both sides of each of these inequalities by the positive number $hyp\,$ , we get $\frac{opp}{hyp} < \frac{hyp}{hyp}\,$ and $\frac{adj}{hyp} < \frac{hyp}{hyp}\,$
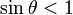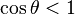
or $\sin \theta < 1\,$ and $\cos \theta < 1\,$

Table

See Table of functions.

Quiz

Trigonometry/Functions/Quiz

Other resources

Reading: w:Trigonometric_Functions (Wikipedia)
Videos:

Basic Trigonometry (Youtube)

Basic Trigonometry II (Youtube)

Trigonometry/Functions/Flash cards

This article is issued from Wikiversity - version of the Thursday, October 16, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.