Topology/Lesson 5
< TopologyDirected Sets
Directed sets are very useful in topology. We will explore a couple of their uses in this lesson.
Definition
A directed set is a set 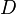 with a partial order denoted by
with a partial order denoted by 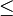 which satisfies the additional requirement that given
which satisfies the additional requirement that given 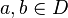 there is
there is 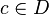 such that
such that 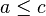 and
and 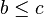 .
.
Examples (directed set)
- Let
 be a set. Then its power set
be a set. Then its power set 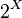 is a directed set, ordered by set inclusion. Indeed, if
is a directed set, ordered by set inclusion. Indeed, if 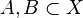 then
then 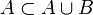 and
and 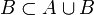 .
. - Suppose that
 is a topological space and
is a topological space and 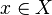 . Then the set
. Then the set 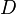 of all neighborhoods of
of all neighborhoods of  is a directed set, ordered by reverse set inclusion (that is,
is a directed set, ordered by reverse set inclusion (that is, 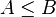 if
if 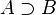 ). The proof is left as an exercise.
). The proof is left as an exercise.
Cofinal set
Let 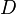 be a directed set. A subset
be a directed set. A subset 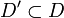 is cofinal if for every
is cofinal if for every 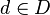 there is
there is 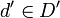 such that
such that 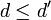 .
.
Examples (cofinal set)
- Let
 be an infinite set. Then, as above, its power set
be an infinite set. Then, as above, its power set 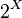 is a directed set. The subset consisting of only infinite subsets of
is a directed set. The subset consisting of only infinite subsets of  is a cofinal set.
is a cofinal set. - As in Example 2 above, let
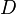 be the set of neighborhoods of the point
be the set of neighborhoods of the point 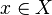 . Then the set of open neighborhoods of
. Then the set of open neighborhoods of  is a cofinal set. If
is a cofinal set. If  is Hausdorff and locally compact, then the set of compact neighborhoods of
is Hausdorff and locally compact, then the set of compact neighborhoods of  is also cofinal.
is also cofinal.
Nets
One of the main applications of directed sets is that of nets. A net is kind of like a sequence, but the indexing set is a directed set rather than an ordinal set (or, specifically the set 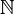 ). That is, a net in a space
). That is, a net in a space  is a function
is a function 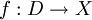 , where
, where 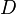 is a directed set.
is a directed set.
Subnet
Let 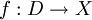 be a net. A subnet of
be a net. A subnet of  is the restriction of
is the restriction of  to a subset
to a subset 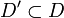 that is also directed and is cofinal in
that is also directed and is cofinal in 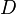 .
.
Nets are like sequences. Just as you can picture a sequence being a bunch of points in a space, and you usually think of that sequences limiting on some particular point, you can think of nets as a bunch of points in a space. And, just like sequences, nets are useful when they accumulate at a specific point (or multiple points).
Limits
Let 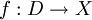 be a net. The net converges to a point
be a net. The net converges to a point 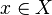 if for every neighborhood
if for every neighborhood 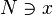 , there is
, there is 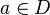 such that
such that 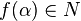 for all
for all 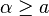 .
.
This definition looks surprisingly similar to the definition of the limit of a sequence, and it is very similar. However, note one significant difference. In 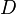 , not all points are assumed to be comparable (that is, there might be
, not all points are assumed to be comparable (that is, there might be 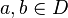 for which neither
for which neither 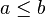 nor
nor 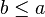 is true). Therefore, the quantifier "for all
is true). Therefore, the quantifier "for all 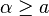 " excludes any point in
" excludes any point in 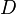 that is not comparable to
that is not comparable to 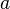 .
.
What's all the hype about? Why did topologists even invent the concept of a net? Consider the following results, prior to nets.
- If a set
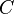 is compact, then every sequence in it has a convergent subsequence.
is compact, then every sequence in it has a convergent subsequence. - If a function
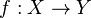 is continuous and
is continuous and 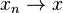 then
then 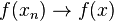 .
. - Let
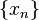 be a sequence in a set
be a sequence in a set 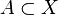 . If
. If 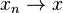 in
in  then
then 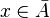 (the closure of
(the closure of 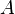 ).
).
Each of these is a very good result. However, for each one the converse is false. Consider the following examples.
- The space
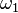 (the ordinal space, which consists of all finite/countable ordinals) is not compact but every sequence in it has a convergent subsequence (in particular, every monotone sequence in
(the ordinal space, which consists of all finite/countable ordinals) is not compact but every sequence in it has a convergent subsequence (in particular, every monotone sequence in 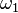 is convergent).
is convergent). - Let
![f:[0,\omega_1]\to \{0,1\}](../I/m/e7ed3de5dbf001d5e66858d9d9dcd24b.png) be defined by
be defined by 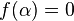 for
for 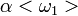 and
and 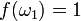 .
. ![[0,\omega_1]](../I/m/eba964dce423d69b1bb9b1ca3484ca29.png) has the order topology, since it is an ordinal, and
has the order topology, since it is an ordinal, and 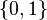 has the discrete topology. Then
has the discrete topology. Then  is not continuous but every sequence in
is not continuous but every sequence in ![[0,\omega_1]](../I/m/eba964dce423d69b1bb9b1ca3484ca29.png) is preserved (that is, if
is preserved (that is, if 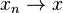 in
in ![[0,\omega_1]](../I/m/eba964dce423d69b1bb9b1ca3484ca29.png) then
then 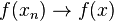 ).
). - The point
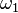 in the space
in the space ![[0,\omega_1]](../I/m/eba964dce423d69b1bb9b1ca3484ca29.png) (as in the previous example) is in the closure of
(as in the previous example) is in the closure of 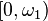 but is not the limit of any sequence in that set.
but is not the limit of any sequence in that set.
However, if we use nets instead of sequences, each of these results becomes a biconditional. The proof of each will be left as an exercise to the student. A suggestion for each would be to follow a proof of the case where only sequences are considered.
Exercises
Prove each of the following.
- A set
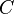 is compact if and only if every net in
is compact if and only if every net in 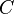 has a convergent subnet.
has a convergent subnet. - A function
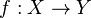 is continuous if and only if
is continuous if and only if 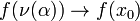 whenever
whenever 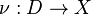 is a net converging to
is a net converging to 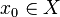 .
. - Let
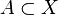 . Then
. Then 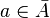 if and only if there is a net in
if and only if there is a net in 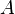 that converges to
that converges to 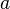 .
.