Topology/Lesson 4
< TopologyIntroduction to Limits
This lesson will introduce the notion of a limit.
Definition (sequence)
A sequence on a topological space  is a function
is a function 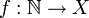 . Alternatively, it is a list
. Alternatively, it is a list 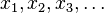 where
where 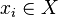 for all
for all 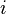 . The sequence is often denoted as
. The sequence is often denoted as 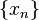
Definition (limit of a sequence)
The point 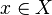 is a limit of the sequence
is a limit of the sequence 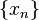 if for every neighborhood
if for every neighborhood 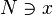 , there is
, there is 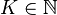 such that
such that 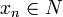 for all
for all 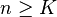 . In this case, we write
. In this case, we write 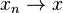 and say that
and say that 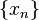 converges to
converges to  .
.
Note that a sequence might have multiple limits. For example, in any space with the indiscrete topology, every sequence converges to every point of the space!
Example
Let 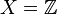 be the set of integers with the topology where
be the set of integers with the topology where 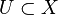 is open if
is open if 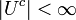 (called the finite complement topology). Let
(called the finite complement topology). Let 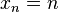 . Then we see that
. Then we see that 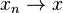 for any
for any 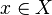 . Indeed, note that given any neighborhood
. Indeed, note that given any neighborhood 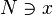 ,
, 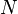 contains all but finitely many points of
contains all but finitely many points of  . Let
. Let 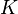 be the maximum of all of the numbers not contained in
be the maximum of all of the numbers not contained in 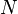 . Then for all
. Then for all 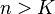 , we see that
, we see that 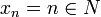 , hence
, hence 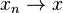 .
.
Theorem
If a space  is Hausdorff and the sequence
is Hausdorff and the sequence 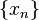 in
in  has a limit, then that limit is unique.
has a limit, then that limit is unique.
The proof of this theorem is left as an exercise to the student. The hint is to assume that there are two distinct limits and show that this leads to a contradiction.
Theorem
If 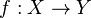 is a continuous function and
is a continuous function and 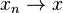 in
in  then
then 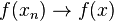 in Y.
in Y.
Proof
Let 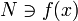 be an open neighborhood of
be an open neighborhood of  . Since
. Since  is continuous,
is continuous, 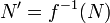 is open in
is open in  and, by definition, contains
and, by definition, contains  . Therefore, there is
. Therefore, there is 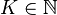 such that
such that 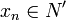 for all
for all 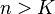 . Therefore,
. Therefore, 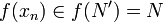 . Thus,
. Thus, 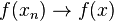 .
.
The converse of this theorem is, in general, false. However, it is true for metric spaces. (In fact, it holds for any first-countable space.)