Topology/Lesson 3
< TopologyMetric Space
A metric space has very many useful properties and they are very good for beginning topology students to study because of their relative intuitive nature.
Definition
Let  be a set. Then a metric on the set
be a set. Then a metric on the set  is a function
is a function 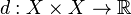 such that
such that
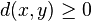 and equality holds if and only if
and equality holds if and only if 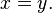
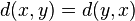 (i.e.,
(i.e., 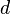 is symmetric).
is symmetric).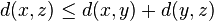 (the triangle inequality).
(the triangle inequality).
We can define a topology on the set  using the metric
using the metric 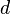 as follows. For
as follows. For 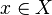 and
and 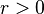 define
define 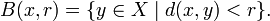 Then take the collection
Then take the collection 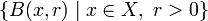 as a basis. Call this topology
as a basis. Call this topology 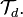
If 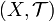 is a topological space, then we say that it is metrizable if there is a metric
is a topological space, then we say that it is metrizable if there is a metric 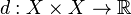 such that
such that 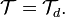 If
If  is metrizable and
is metrizable and 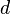 is such a metric then we call the pair
is such a metric then we call the pair 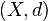 a metric space.
a metric space.
Examples
- The most obvious example is the space
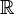 together with the metric
together with the metric 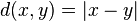 which is called the standard metric on
which is called the standard metric on 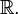
- Any set has a metric on it. As an example, let
 be any set and let
be any set and let 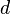 be given by
be given by 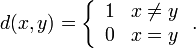 It is left as an exercise to check that this is a metric, called the discrete metric because the topology it gives
It is left as an exercise to check that this is a metric, called the discrete metric because the topology it gives  is the discrete topology.
is the discrete topology.
Exercises
- Show that the discrete metric is a metric and that it gives the discrete topology on
Isometries
The "isomorphism" in the category of topological spaces is homeomorphism, as we saw in Lesson 2. The "isomorphism" in the category of metric spaces is called "global isometry" and is much more strict than homeomorphism.
Definition
Let 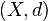 and
and 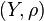 be metric spaces. Then a function
be metric spaces. Then a function 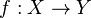 is called an isometry if for all
is called an isometry if for all 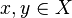 we have
we have 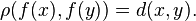 If
If  is also surjective, then we say that
is also surjective, then we say that  is a global isometry.
is a global isometry.
Examples
- If
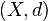 is any metric space, then the identity map is an isometry.
is any metric space, then the identity map is an isometry. - If
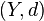 is a metric space and
is a metric space and  then the inclusion map
then the inclusion map 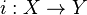 is an isometry.
is an isometry.
Exercises
- Show that every isometry is injective and therefore every global isometry is bijective.
- Show that every isometry is an embedding and therefore every global isometry is a homeomorphism.
- Find a function that is a homeomorphism but not an isometry.