Topology/Lesson 2
< TopologySo in the first lesson we learned what a topology is, what open sets, closed sets, and bases are. You should be comfortable with these concepts before beginning this second lesson.
Continuous Function
We will define the notion of a continuous function below. (Note that in topological texts and papers it is common to use the word 'map' and even the word 'function' to mean a continuous function. To avoid ambiguity, in this course we will reserve the word 'function' to mean any function, but will use 'map' to mean a continuous function.)
Definition
Let 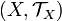 and
and 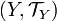 be topological spaces. A function
be topological spaces. A function 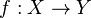 is called continuous if for every
is called continuous if for every 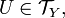 we have
we have 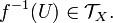 That is, f is continuous iff the f-preimage of every open set (in
That is, f is continuous iff the f-preimage of every open set (in 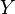 ) is open (in
) is open (in  ).
).
Examples
It is immediate from the definition that the following two types of functions are always continuous. The proof of these two claims is left as an exercise.
- If
 is a discrete space and
is a discrete space and  is any space, then any function
is any space, then any function  is continuous.
is continuous. - If
 is any space and
is any space and 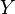 has the indiscrete topology, then any function
has the indiscrete topology, then any function 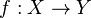 is continuous.
is continuous.
Continuous at a point
It is also possible to talk about a function being continuous at a point of its domain. So, given a map 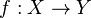 and a point
and a point 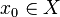 we say that
we say that  is continuous at
is continuous at 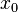 if given any neighborhood
if given any neighborhood 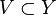 of
of 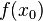 there is a neighborhood
there is a neighborhood 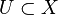 of
of 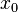 such that
such that 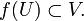
Exercises
Let 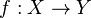 be a function. Show that the following are equivalent.
be a function. Show that the following are equivalent.
 is continuous.
is continuous. is continuous at
is continuous at 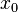 for all
for all 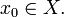
- For any closed set
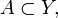 we have
we have 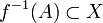 is closed in
is closed in 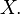
- If
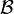 is a basis for
is a basis for 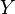 then for any set
then for any set 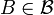 we have
we have 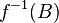 is open in
is open in 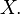
Open maps
The definition of a continuous map may seem awkward. Since it is a morphism in the category of topological spaces, one would expect it to preserve some property about open sets, but what one might first think is that open sets are preserved under the map of the function. But this gives a different concept.
Definition (open map)
Let 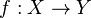 be a continuous function. Then we say that
be a continuous function. Then we say that  is an open map if for any open set
is an open map if for any open set 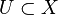 we have
we have 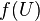 is open in
is open in 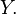
Merely for the purposes of the discussion here, define an open function to be a function (not necessarily continuous) 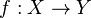 such that
such that 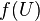 is open in
is open in 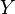 whenever
whenever 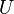 is open in
is open in 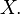
Exercises
- Construct finite-point spaces
 and
and 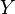 and a map
and a map 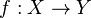 that is continuous but not open.
that is continuous but not open. - Construct another function
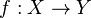 that is not continuous but is an 'open function'.
that is not continuous but is an 'open function'. - Show that the identity map
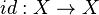 is always continuous and open.
is always continuous and open. - Suppose that
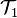 and
and 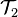 are two distinct topologies on the set
are two distinct topologies on the set 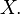 Suppose that the identity map
Suppose that the identity map 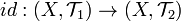 is continuous. Show that
is continuous. Show that 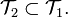 In this case, we say that
In this case, we say that 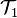 is finer than
is finer than 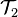 or that
or that 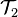 is coarser than
is coarser than 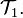
Homeomorphism
The "isomorphism" or "equivalence" of topological spaces is called "homeomorphism." This is analogous to bijection in the case of sets and group isomorphism in the case of groups. Topologically speaking, two spaces are indistinguishable if they are homeomorphic.
Definition
Let 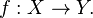 Then we say that
Then we say that  is a homeomorphism if it is bijective and both
is a homeomorphism if it is bijective and both  and
and 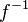 are continuous. In this case we say that
are continuous. In this case we say that  and
and 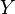 are homeomorphic and sometimes write
are homeomorphic and sometimes write 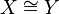 or
or 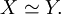
Examples
- If
 is any topological space then the identity map
is any topological space then the identity map 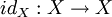 is a homeomorphism.
is a homeomorphism. - If
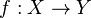 is injective and
is injective and  and
and 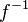 are both continuous then
are both continuous then  is called an embedding. In this case the map
is called an embedding. In this case the map  given by
given by 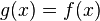 is a homeomorphism. That is, an embedding is a homeomorphism with its image in the target space.
is a homeomorphism. That is, an embedding is a homeomorphism with its image in the target space. - The map
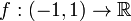 given by
given by 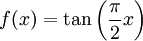 is a homeomorphism.
is a homeomorphism.
Exercises
- Show that the maps given in the examples are indeed homeomorphisms.
- Show that if
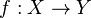 is a homeomorphism then
is a homeomorphism then 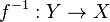 is also a homeomorphism.
is also a homeomorphism. - Show that if
 is homeomorphic to
is homeomorphic to 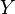 and
and 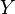 is homeomorphic to
is homeomorphic to 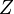 then
then  is homeomorphic to
is homeomorphic to 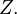 Note that these first 3 exercises show that homeomorphism is an equivalence relation.
Note that these first 3 exercises show that homeomorphism is an equivalence relation.