Numerical Analysis/Romberg Quiz

<quiz>

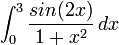{ $\int_0^3 \frac{sin(2x)}{1+x^2}\,dx$ |type="()"} - -1.2345435 + 0.4761463020 - 0.2345632784 - 0.567894567

{ Romberg Integration is an extrapolation formula of the trapezoidal rule for integration. |type="()"} +TRUE. -FALSE.

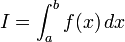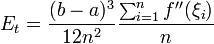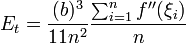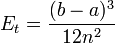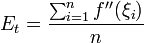
{True error in a multiple segment Trapezoidal rule with n segments for an integral $I = \int_a^b f(x) \,dx$ is |type="()"} + $E_t = \frac{(b-a)^3}{12n^2}\frac{\sum_{i=1}^nf''(\xi_i)}{n}$ - $E_t = \frac{(b)^3}{11n^2}\frac{\sum_{i=1}^nf''(\xi_i)}{n}$ - $E_t = \frac{(b-a)^3}{12n^2}$ - $E_t = \frac{\sum_{i=1}^nf''(\xi_i)}{n}$

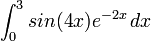{ $\int_0^3 sin(4x)e^{-2{x}}\,dx$ |type="()"} +0.1997146621 -0.1345234567 -0.2345234234 -1.0000000000

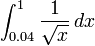{ $\int_{0.04}^1 \frac{1}{\sqrt{x}}\,dx$ |type="()"} -2.6 +1.6 -4.6 -5.6

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.