Numerical Analysis/Romberg Example

Use Romberg Integration to compute 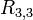$R_{3,3}$ for the following integral
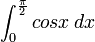
$\int_{0}^{\frac{\pi}{2}}cos x \,dx$

Solution:

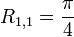
$R_{1,1} = \frac{\pi}{4}[cos(0)+cos(\frac{\pi}{2})]$

$R_{1,1} = \frac{\pi}{4}$

$R_{2,1} = \left(\frac{1}{2}\right)[R_{1,1}+h_{1}f(a+h_{2})]$

$R_{2,1} = \left(\frac{1}{2}\right)[\frac{\pi}{4}+\frac{\pi}{2}cos\left(\frac{\pi}{4}\right)]$
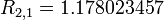
$R_{2,1} = 1.178023457$

$R_{3,1} = \left(\frac{1}{2}\right)[R_{2,1}+h_{2}(f(a+h_{3})+f(a+3h_{3}))]$
$R_{3,1} = \left(\frac{1}{2}\right)[1.178023457+\frac{\pi}{4}(cos(\frac{\pi}{8})+cos(\frac{3\pi}{8})]$
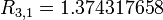
$R_{3,1} = 1.374317658$

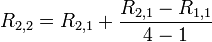
$R_{2,2} = R_{2,1}+ \frac{R_{2,1}-R_{1,1}}{4-1}$
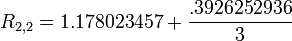
$R_{2,2} = 1.178023457 + \frac{.3926252936}{3}$
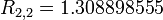
$R_{2,2} = 1.308898555$

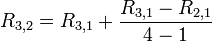
$R_{3,2} = R_{3,1} + \frac{R_{3,1}-R_{2,1}}{4-1}$
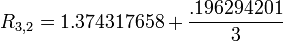
$R_{3,2} = 1.374317658 + \frac{.196294201}{3}$
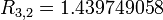
$R_{3,2} = 1.439749058$

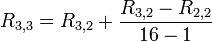
$R_{3,3} = R_{3,2} + \frac{R_{3,2}-R_{2,2}}{16-1}$
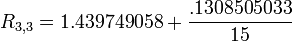
$R_{3,3} = 1.439749058 + \frac{.1308505033}{15}$
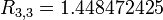
$R_{3,3} = 1.448472425$

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.