Numerical Analysis/Newton form exercise

< Numerical Analysis

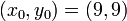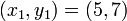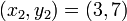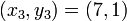1. Using the Newton form, find the interpolating polynomial passing through the points $(x_{0},y_{0}) = (9,9)$ , $(x_{1},y_{1}) = (5,7)$ , $(x_{2},y_{2}) = (3,7)$ , and $(x_{3},y_{3}) = (7,1)$ .

Solution:

To find the four coefficients, we can use the divided differences.

\begin{matrix} x_i&y_i& [y_0,y_1] & [y_0,y_1,y_2] & [y_0,y_1,y_2,y_3] \\ 9 & 9 & & \\ & & {7-9\over 5-9} = {1\over 2} & \\ 5 & 7 & & {{0 - 1\over 2}\over {3-9}} = {1\over 12} \\ & & {7-7\over 3-5} = {0} & &{{{-3\over 4} - {1\over12}}\over {7-9}} = {5\over 12}\\ 3 & 7 & & {{-3\over 2} - 0\over {7-5}} = {-3\over 4} \\ & & {1-7\over 7-3} = {-3\over2} & \\ 7 & 1 & & \\ \end{matrix}

Thus, the four coefficients are 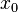$x_{0}$ and the upper diagonal of the calculated divided differences.

Using the Newton Forward Divided Difference formula, we find the polynomial is

p_3(x) = [y_0] + [y_0,y_1](x-x_0) + [y_0,y_1,y_2](x-x_0)(x-x_1) + [y_0,y_1,y_2,y_3](x-x_0)(x-x_1)(x-x_2).

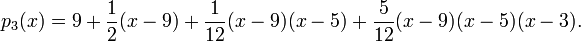
p_3(x) = 9 + \frac{1}{2}(x-9) + \frac{1}{12}(x-9)(x-5) + \frac{5}{12}(x-9)(x-5)(x-3).

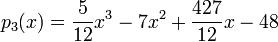p_3(x) = \frac{5}{12}x^{3} - 7x^{2} + \frac{427}{12}x -48

2. Find the interpolating polynomial passing through the four points given in the exercise above as well as through the point 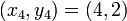$(x_{4},y_{4}) = (4,2)$

Solution:

To find the new coefficient, we can simply add the new point to the end and calculate $[y_0,y_1,y_2,y_3,y_4]$ .

\begin{matrix} x_i&y_i & [y_0,y_1] & [y_0,y_1,y_2] & [y_0,y_1,y_2,y_3] & [y_0,y_1,y_2,y_3,y_4] \\ 9 & 9 & & \\ & & {1\over 2} & \\ 5 & 7 & & {1\over 12} \\ & & {0} & &{5\over 12}\\ 3 & 7 & & {-3\over 4} & & {{{-23\over 12} - {5\over 12}}\over {4-9}} = {17\over 15} \\ & & {-3\over2} & & {{{7\over 6} - {-3\over 4}}\over {4-5}} = {-23\over 12} \\ 7 & 1 & & {{-1\over 3} - 0\over {-3\over 2}} = {7\over 6} \\ & & {2-1\over 4-7} = {-1\over 3} & \\ 4 & 2 & & \\ \end{matrix}

Thus, we find the polynomial 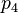$p_{4}$ is

p_4(x) = p_3 + [y_0,y_1,y_2,y_3,y_4](x-x_0)(x-x_1)(x-x_2)(x-x_3).

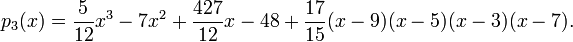
p_3(x) = \frac{5}{12}x^{3} - 7x^{2} + \frac{427}{12}x -48 + \frac{17}{15}(x-9)(x-5)(x-3)(x-7).

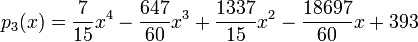p_3(x) = \frac{7}{15}x^{4} - \frac{647}{60}x^{3} + \frac{1337}{15}x^{2}-\frac{18697}{60}x + 393

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.