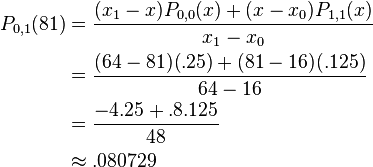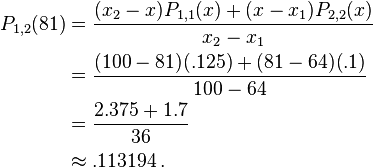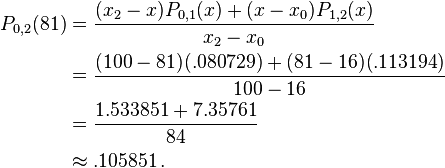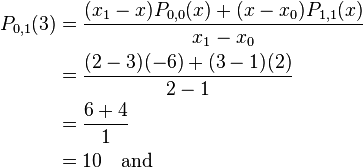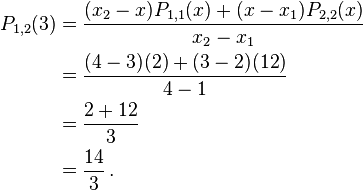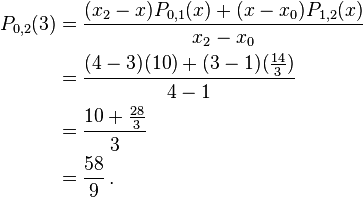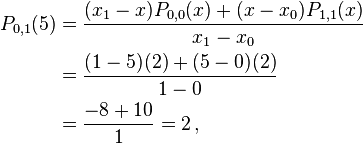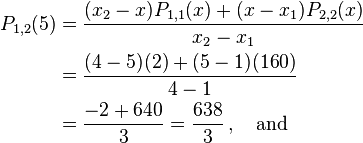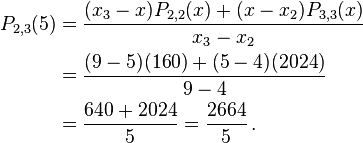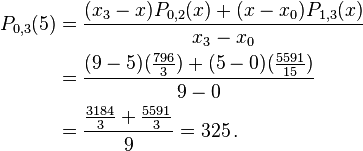Numerical Analysis/Neville's algorithm examples
< Numerical AnalysisThe main idea of Neville's Algorithm is to approximate the value of a polynomial at a particular point without having to first find all of the coefficients of the polynomial. The following examples and exercise illustrate how to use this method.
Example 1
Approximate the function 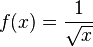 at
at 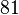 using
using 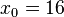 ,
, 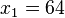 , and
, and 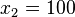 .
.
We begin by finding the value of the function at the given points, 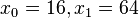 , and
, and 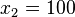 . We obtain
. We obtain
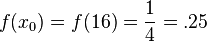
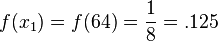 and
and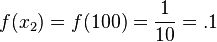 .
.
Since, we know from the Wikipedia page on Neville's Algorithm that 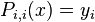 , the approximations for
, the approximations for 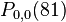 ,
, 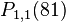 and
and 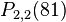 are
are
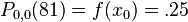
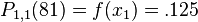 and
and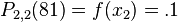 .
.
Using Neville's Algorithm we can now calculate 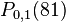 and
and 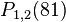 . We find
. We find 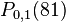 and
and 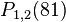 to be
to be
and
From these two values we now find 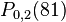 to be
to be
Thus, our approximation for the function 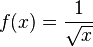 at
at 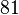 using
using 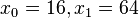 , and
, and 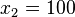 is
is 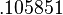 . We know the actual value of the function evaluated at
. We know the actual value of the function evaluated at 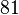 is
is 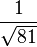 or
or 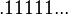 . Therefore, our approximation within
. Therefore, our approximation within 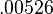 of the actual value.
of the actual value.
Example 2
For this example, we will use the points given in the example of Newton form to approximate the function  at
at 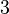 . The given points are
. The given points are
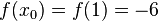
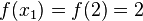 and
and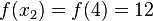 .
.
Using 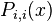 , the approximations for
, the approximations for 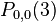 ,
, 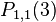 and
and 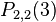 are
are
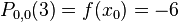
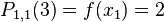 and
and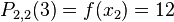 .
.
Using Neville's Algorithm we now calculate 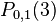 and
and 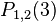 to be equal to
to be equal to
From these two values we find 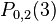 to be
to be
Exercise
Try this one on your own before revealing the answer. You can reveal one step at a time.
Approximate the function 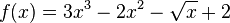 at
at 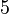 using
using 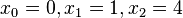 , and
, and 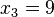 .
.
Solution:
Step 1:
We begin by evaluating the function at four given points and obtain
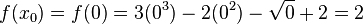
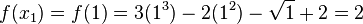
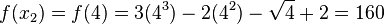 and
and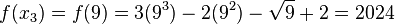 .
.
Thus, 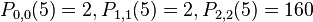 and
and 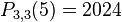 .
.
Step 2:
We can calculate 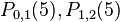 and
and 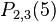 to be
to be
Step 3:
From these values we now find 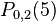 , and
, and 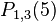 and get
and get
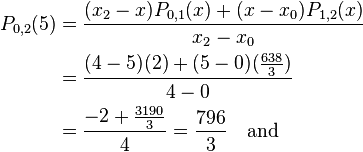
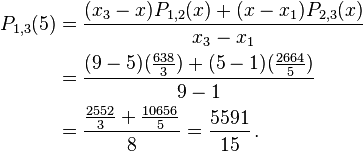 .
.
Step 4:
Finally, we can find 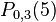 to be
to be
References
http://people.math.sfu.ca/~kevmitch/teaching/316-10.09/neville.pdf