Numerical Analysis/Lagrange exercise
< Numerical AnalysisFind the interpolating polynomial passing through the points 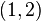 ,
, 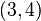 ,
, 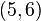 ,
, 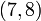 , using the Lagrange method.
, using the Lagrange method.
Solution:
By using the Lagrange method, we need to find the lagrange basis polynominals first.Since we know
So we can get the basis polynominals as following:
Thus the interpolating polynomial then is:
Therefore, we get the Lagrange form interpolating polynomial:
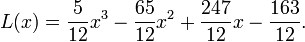
This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
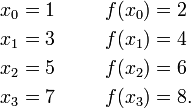
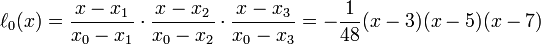
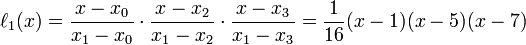
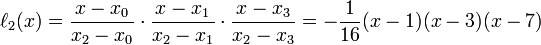
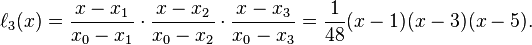
![\begin{align}
L(x)&=f(x_0)\ell_0(x)+f(x_1)\ell_1(x)+f(x_2)\ell_2(x)+f(x_3)\ell_3(x)\\[10pt]
&=2\cdot{1\over 16}(x-1)(x-5)(x-7)+4\cdot{-1\over 16}(x-1)(x-3)(x-7)+6\cdot{-1\over 16}(x-1)(x-3)(x-7)+8\cdot{1\over 48}(x-1)(x-3)(x-5)\\[10pt]
&= \frac{5}{12}x^{3} - \frac{65}{12}x^{2} + \frac{247}{12}x - \frac{163}{12} .
\end{align}](../I/m/04a200e42e6cb58ac122aecd1f9c29d5.png)