Numerical Analysis/Lagrange example

< Numerical Analysis

We'll find the interpolating polynomial passing through the points 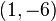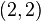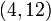$(1,-6)$ , $(2,2)$ , $(4,12)$ , using the Lagrange method.

We first use the formula to write the following:

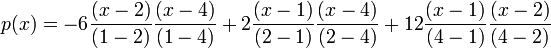
$p(x) = -6\frac{(x-2)}{(1-2)}\frac{(x-4)}{(1-4)} + 2\frac{(x-1)}{(2-1)}\frac{(x-4)}{(2-4)} + 12\frac{(x-1)}{(4-1)}\frac{(x-2)}{(4-2)}$

After some simplification, we get:

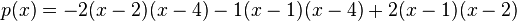
$p(x) = -2(x-2)(x-4) - 1(x-1)(x-4) + 2(x-1)(x-2)$

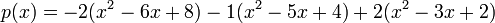
$p(x) = -2(x^{2} -6x +8) -1(x^{2} -5x +4) +2(x^{2}-3x +2)$

And our answer:

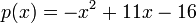$p(x) = -x^{2} +11x -16$ .

Adding a point

Now we'll add a point to our data set, and find a new interpolating polynomial. Let us add the point 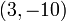$(3,-10)$ to our set. Starting over with the Lagrange formula, we write:

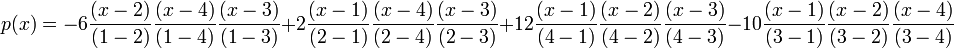
$p(x) = -6\frac{(x-2)}{(1-2)}\frac{(x-4)}{(1-4)}\frac{(x-3)}{(1-3)} + 2\frac{(x-1)}{(2-1)}\frac{(x-4)}{(2-4)}\frac{(x-3)}{(2-3)} + 12\frac{(x-1)}{(4-1)}\frac{(x-2)}{(4-2)}\frac{(x-3)}{(4-3)} - 10\frac{(x-1)}{(3-1)}\frac{(x-2)}{(3-2)}\frac{(x-4)}{(3-4)}$

Simplifying, we get:

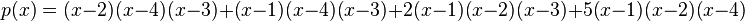
$p(x) = (x-2)(x-4)(x-3) + (x-1)(x-4)(x-3) +2(x-1)(x-2)(x-3) + 5(x-1)(x-2)(x-4)$

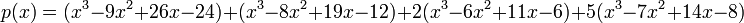
$p(x) = (x^{3} - 9x^{2} + 26x -24) + (x^{3} - 8x^{2} + 19x -12) + 2(x^{3} -6x^{2} + 11x -6) + 5(x^{3} -7x^{2} +14x -8)$

And our polynomial is:

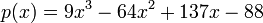$p(x) = 9x^{3} -64x^{2} + 137x -88$ .

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.