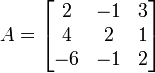Numerical Analysis/LU decomposition exercises

< Numerical Analysis

LU Decomposition exercises and quiz

Exercise 1


Problem
Given the 3x3 matrix:

A = \begin{bmatrix} 2&-1&3\\4&2&1\\-6&-1&2\end{bmatrix}

Find LU decomposition of A


Solution
The procedure of LU decomposition runs similar to the process of Gaussian Elimination. Firstly A is reduced to upper triangular form, which is U, using just the third elementary row operation, namely: add to one row of matrix a scalar time another row of that same matrix. Those scalar used during this process are co-efficient in the L matrix.

The final result will look like this: 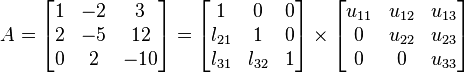A = \begin{bmatrix} 1&-2&3\\2&-5&12\\0&2&-10\end{bmatrix}= \begin{bmatrix} 1&0&0\\l_{21}&1&0\\l_{31}&l_{32}&1\end{bmatrix} \times \begin{bmatrix} u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{bmatrix}.

Here are the solution for this problem:

According to Gaussian Elimination, the first number in row 2 must be zero-out by adding the first row of matrix a scalar times second row. This scalar, fortunately, is 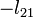- l_{21}.

Therefore:

1.

\displaystyle \ l_{21} = .
And A \rightarrow A1 = \begin{bmatrix} 2&-1&3\\0&4&-5\\-6&-1&2\end{bmatrix} .
In the similar manner we have:
\displaystyle \ l_{31} = .
And A1 \rightarrow A2 = \begin{bmatrix} 2&-1&3\\0&4&-5\\0&-4&11\end{bmatrix}
\displaystyle \ l_{32} = .
And A2 \rightarrow A3 = U = \begin{bmatrix} 2&-1&3\\0&4&-5\\0&0&6\end{bmatrix} .
Eventually, A has been factorized to LU:
A = \begin{bmatrix} 2&-1&3\\4&2&1\\-6&-1&2\end{bmatrix}= \begin{bmatrix} 1&0&0\\**&1&0\\**&*&1\end{bmatrix}\times \begin{bmatrix} 2&-1&3\\0&4&-5\\0&0&6\end{bmatrix}.

Your score is 0 / 0

Exercise 2

Use exercise 1's result to solve the system:

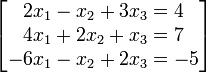
\begin{bmatrix} 2x_1-x_2+3x_3=4\\4x_1+2x_2+x_3=7\\-6x_1-x_2+2x_3=-5 \end{bmatrix}

Solution:

The idea of using LU decomposition to solve systems of simultaneous linear equations Ax=b is rewriting the systems as L(Ux)=b. To solve x, we first solve the systems Ly=b for y, and then, once y is determined, we solve the systems: Ux=y for x. Both systems are easy to solve, the first by forward substitution and the second by backward substitution.

Here is the solution for this exercise:

This system has the matrix form:

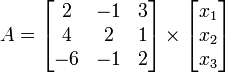A = \begin{bmatrix} 2&-1&3\\4&2&1\\-6&-1&2\end{bmatrix} \times \begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix} 4\\7\\-5\end{bmatrix}.

Since 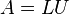A = LU, by Exercise 1 we have:

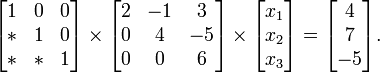
\begin{bmatrix} 1&0&0\\**&1&0\\**&*&1\end{bmatrix} \times \begin{bmatrix} 2&-1&3\\0&4&-5\\0&0&6\end{bmatrix}\times \begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix} 4\\7\\-5\end{bmatrix}.

Lets 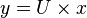y = U\times x, we have:

\begin{bmatrix} 1&0&0\\**&1&0\\**&*&1\end{bmatrix} \times \begin{bmatrix} y_1\\y_2\\y_3\end{bmatrix} = \begin{bmatrix} 4\\7\\-5\end{bmatrix} .

Use forward substitution we have:

1.

\displaystyle \ y_1 =
\displaystyle \ y_2 =
\displaystyle \ y_3 =
Next, since Ux = y, we have
\begin{bmatrix} 2&-1&3\\0&4&-5\\0&0&6\end{bmatrix} \times \begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix} y_1\\y_2\\y_3\end{bmatrix} .
Use backward substitution we have:
\displaystyle \ x_1 =
\displaystyle \ x_2 =
\displaystyle \ x_3 =

Your score is 0 / 0
This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.