Numerical Analysis/Inverse iteration exercises

< Numerical Analysis

Consider the matrix, $A=\left[\begin{array}{c c c}6 & 2 & -1 \\2 & 5 & 1 \\-1 & 1 & 4 \end{array} \right]$ , and the vector, $\textbf{x}^{(0)} = \left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right].$

The LU decomposition of A is $L=\left[\begin{array}{c c c} 1&0&0\\0.3333&1&0\\-0.167&0.3077&1\end{array}\right], ~~ U=\left[\begin{array}{c c c}6&2&-1\\0&4.333&1.333\\0&0&3.423\end{array}\right]$ .

By hand, use the LU decomposition to do two iterations of the inverse power method (without shift) starting with 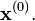$\textbf{x}^{(0)}.$

Solution, first iteration:

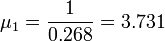$LU\textbf{y}^{(1)}=\textbf{x}^{(0)} \Rightarrow \textbf{y}^{(1)}=\left[\begin{array}{c}0.1804\\0.0736\\0.268\end{array}\right]$ . The estimated eigenvalue is $\mu_1 = \frac{1}{0.268}=3.731$ and the estimated eigenvector is $\textbf{x}^{(1)}= \frac{\textbf{y}^{(1)}}{0.2678} = \left[ \begin{array}{c} 0.6800 \\ 0.2400 \\ 1.0000 \end{array} \right]$ .

Solution, second iteration:

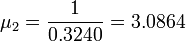$LU\textbf{y}^{(2)}=\textbf{x}^{(1)} \Rightarrow \textbf{y}^{(2)}=\left[\begin{array}{c}0.1996\\-0.0966\\0.3240\end{array}\right]$ . The estimated eigenvalue is $\mu_2 = \frac{1}{0.3240}=3.0864$ and the estimated eigenvector is $\textbf{x}^{(2)} = \frac{\textbf{y}^{(2)}}{0.3240} = \left[ \begin{array}{c} 0.6158 \\ -0.2982 \\ 1.0000 \end{array} \right]$ .

Use a computational software package to do 50 iterations. What was the result?

Solution, 50 iterations:

The estimated eigenvalue after 50 iterations is 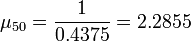$\mu_{50} = \frac{1}{0.4375}=2.2855$ and the estimated eigenvector is $\textbf{x}^{(50)} = \left[ \begin{array}{c} 0.7750 \\ -0.9394 \\ 1.0000 \end{array} \right]$ .

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.