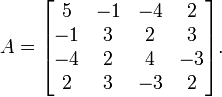Numerical Analysis/Householder transformation exercises

< Numerical Analysis

Householder's method Exercises

Exercise 1

This exercise will help you in introducing how to perform the Householder's method to transform a symmetric matrix A into the tridiagonal form. All of the notations and computations in this Exercise follow from those in Section 9.3, Numerical Analysis, Burden and Faires, 8th Edition. It's recommended that you read that section before solving the problem. It's also recommended that you read the following useful links
1. Householder's method for symmetric matrices, J. H. Wilkinson, Handbook Series Linear Algebra, Volume 4, Number 1 / December, 1962, Springer Berlin / Heidelberg.
2. Module for Householder Transformations, Mathematics Department, California State University, Fullerton.


Problem
Let

A = \begin{bmatrix} 5&-1&-4&2\\-1&3&2&3\\-4&2&4&-3\\2&3&-3&2 \end{bmatrix}.

Perform Householder's method to bring A into a tridiagonal form.

Solution

Step 1: k = 1 (Meaning: Making 0's for the third and fourth rows of the first column)

1.

\displaystyle \alpha = -sgn(a_{k+1,k})\sqrt{\sum_{j=k+1}^{n}a_{jk}^2} is .

2.

r = \sqrt{\frac{1}{2}(\alpha^{2}-a_{k+1,k}\alpha)} is .

3.

Now, we are going to find the vector w^{(1)} = \begin{bmatrix} w^{(1)}_1\\w^{(1)}_2\\w^{(1)}_3\\w^{(1)}_4 \end{bmatrix}
Set w^{(1)}_1 = 0, we need to find w^{(1)}_2, w^{(1)}_3, w^{(1)}_4
w^{(1)}_2 = \frac{a_{2,1}-\alpha}{2r} = .
w^{(1)}_j = \frac{a_{j,1}}{2r} for j = 3 and 4 gives
w^{(1)}_3 = \frac{a_{3,1}}{2r} =
w^{(1)}_4 = \frac{a_{4,1}}{2r} =

4.

The orthogonal matrix \displaystyle P^{1} , defined as \displaystyle P^{1} = I - 2w^{(1)}(w^{(1)})^t is (click Submit to see the answer)
→ P^{1} = \begin{bmatrix} 1&0&0&0\\0&-0.2182&-0.8729&0.4364\\0&-0.8729&0.3746&0.3127\\0&0.4364&0.3127&0.8436 \end{bmatrix}.

5.

The new matrix \displaystyle A^{(1)} , defined as \displaystyle A^{(1)} = P^{1}AP^{1}, should be in the form A^{(1)} = \begin{bmatrix} *&*&0&0 \\ **&*&*&* \\0&*&*&*\\0&*&*&*\end{bmatrix}
→ A^{(1)} = \begin{bmatrix} 5&4.5826&0&0\\4.5826&6.0476&-0.1222&0.2793\\0&-0.1222&-0.6059&-3.4068\\0&0.2793&-3.4068&3.5582\end{bmatrix}
This is the end of Step 1.

Your score is 0 / 0



Step 2: k = 2 (Meaning: Making 0's for the fourth row of the second column)
In Step 2, we redo the computations in Step 1 with the matrix 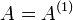\displaystyle A = A^{(1)}

1.

\displaystyle \alpha = -sgn(a_{k+1,k})\sqrt{\sum_{j=k+1}^{n}a_{jk}^2} is .

2.

r = \sqrt{\frac{1}{2}(\alpha^{2}-a_{k+1,k}\alpha)} is .

3.

Now, find the vector w^{(2)} = \begin{bmatrix} w^{(2)}_1\\w^{(2)}_2\\w^{(2)}_3\\w^{(2)}_4 \end{bmatrix}
Set w^{(2)}_1 = w^{(2)}_2 = 0, we need to find w^{(2)}_3, w^{(2)}_4
w^{(2)}_3 = \frac{a_{2,1}-\alpha}{2r} = .
w^{(2)}_4 = \frac{a_{4,1}}{2r} =

4.

The orthogonal matrix \displaystyle P^{2} , defined as \displaystyle P^{2} = I - 2w^{(2)}(w^{(2)})^t is (click Submit to see the answer)
→ P^{2} = \begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&-0.4009&0.9161\\0&0&0.9161&0.4009 \end{bmatrix}.

5.

The new matrix \displaystyle A^{(2)} , defined as \displaystyle A^{(2)} = P^{2}A^{(1)}P^{2}, should be in the form A^{(2)} = \begin{bmatrix} *&*&0&0\\**&*&*&0\\0&*&*&*\\0&0&*&*\end{bmatrix}
→ A^{(2)} = \begin{bmatrix} 5&4.5826&0&0\\4.5826&6.0476&0.3049&0\\0&0.3049&5.3914&-0.7824\\0&0&-0.7824&-2.4390\end{bmatrix}
This is the end of Step 2.

Your score is 0 / 0

Now the matrix 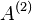\displaystyle A^{(2)} is in a tridiagonal form. The Householder's method is complete.

Exercise 2

1. Householder's method is for

Any matrix.
A non-symmetric positive define matrix.
A symmetric matrix.
A non-symmetric diagonally dominant matrix.

2. The goal of Householder's method is for

Finding the determinant of a matrix.
Transforming a matrix to tridiagonal form.
Finding eigenvalues of a matrix.
Finding the LU decomposition of a matrix.

3. How many steps do we need to perform in Householder's method

n steps (where n is the size of the matrix).
2n steps.
\frac{n}{2} steps.
n-2 steps.

4. What should be performed after Householder's method

LU decomposition.
Support Vector Decomposition (SVD).
Power method.
QR decomposition.

5. Will the Householder's method ever fail

Yes
No.

Your score is 0 / 0

Exercise 3

Problem
Based on the computations performed in Exercise 1, write code in Matlab to perform the Householder's method for an input symmetric matrix A.


Solution

→ 
% Get the size of the matrix A
[n m] = size(A);
% Define the Identity matrix of size of A
I = diag(ones(1,n));
% Householder's method with details
for k = 1 : (n-2)
    % Define the vector w. Initially, w is a zero vector
    w = zeros(n,1);
    % Compute \alpha^2
    alpha_square = sum(A(k+1:n,k)'*A(k+1:n,k))
    % Get \alpha with the appropriate sign
    ap = -sign(A(k+1,k))*sqrt(alpha_square)
    % Find r
    r = sqrt((alpha_square-A(k+1,k)*ap)/2)
    r2 = 2*r;
    % Find w(k+1)
    w(k+1) = (A(k+1,k)-ap)/r2;
    % Find w(j) for j from k+2 to n
    for j = (k+2) : n
        w(j) = A(j,k)/r2;
    end;
    w
    % From the orthogonal matrix P
    P = I - 2*w*w'
    % Update the matrix A
    A = P*A*P
end;

Your score is 0 / 0


132.235.39.18 19:02, 28 May 2009 (UTC) Nam Nguyen

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.