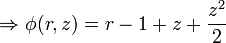Numerical Analysis/stability of RK methods/exercises
< Numerical Analysis < stability of RK methodsExercises
Ex:1
find the stability function for RK2 which is given by:
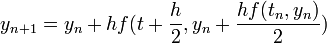
Solution:
applying this method to the test equation 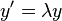
- we get
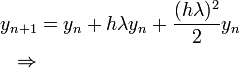
the stability polynomial 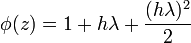
Ex:2
find the absolute stability region for RK2.
Solution:
by setting 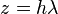
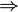 the abs.stability region is given by
the abs.stability region is given by 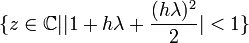
Ex:3
find the characteristic polynomial for RK2.
Solution:
it is 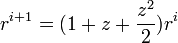 divide both sides of the equation by
divide both sides of the equation by 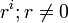 you get
you get 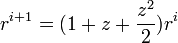
Ex:4
is RK2 stable, if it is what type of stability.
Solution:
you get 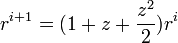 by setting z=0,
by setting z=0,
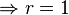
- so the method is strongly stable since r=1, is the only root, and has a value of 1.
Ex:5
Determine the stability of Back ward Euler method.
Solution:
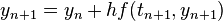
- by applying this method to the test equation
- then
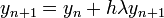
- and so
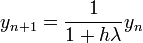
- call
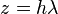 and so:
and so: 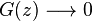 as
as 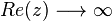
- and so this is L-Stable method when applied to stiff equation.
This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.