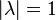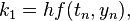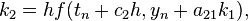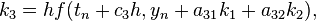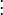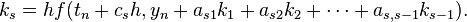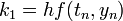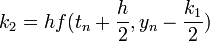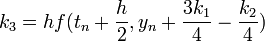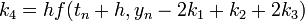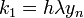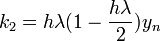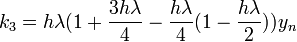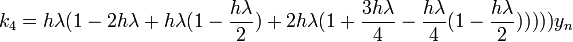Numerical Analysis/stability of RK methods

Definitions

let 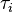$\tau_i$ is the local truncation error, and k is the number of time steps, then:

The numerical method is consistent with a differential equation if
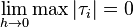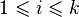$\lim_{h \to 0} \operatorname{max}|\tau_i|=0$ over $1\leqslant i \leqslant k$ .

according to this definition w:Euler's method is consistent.
A numerical method is said be convergent with respect to differential equation if
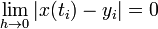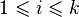$\lim_{h \to 0}|x(t_i)-y_i|=0$ over $1\leqslant i \leqslant k$ ;

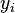where $y_i$ is the approximation for $x(t_i)$ .
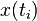A numerical method is stable if small change in the initial conditions or data, produce a correspondingly small change in the subsequent approximations.

Theorem: For an initial value problem

x'=f(t,x)

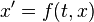with

t\in[t_0,t_0+\alpha]

and certain initial conditions, 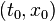$(t_0,x_0)$ , let us consider a numerical method of the form

(y_0=x_0)

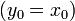and

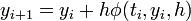y_{i+1}=y_i+h\phi(t_i,y_i,h)

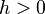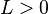If there exists a value $h>0$ such that it is continuous on the iterative domain, $\Omega$ and if there exists an $L>0$ such that

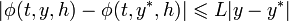|\phi(t,y,h)-\phi(t,y^*,h)|\leqslant L |y-y^*|

for all

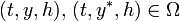(t,y,h),\,(t,y^*,h)\in \Omega

the method fulfills the w:Lipschitz condition, and it is stable and convergent if and only if it is consistent. That is,

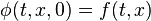\phi(t,x,0)=f(t,x)

for all

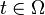t \in \Omega

For a similar argument, one can deduce the following for multi- step methods:

The method is stable if and only if all roots, 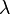$\lambda$ , of the characteristic polynomial satisfy
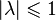$|\lambda|\leqslant 1$ ,

and any root of

$|\lambda|=1$

is simple root.
one more result is that if the method is consistent with the differential equation, the method is stable if and only if it it is convergent.

see

stability polynomials of Runge-Kutta methods

The w:Runge–Kutta methods are very useful in solving systems of differential equations, it has wide applications for the scientists and the engineers, as well as for the economical models, the recognized with their practical accuracy where we can use and get very good results and approximations when solving an ODE problem, RK has the general form :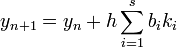 $y_{n+1} = y_n + h\sum_{i=1}^s b_i k_i$ , where

k_1 = hf(t_n, y_n), \,

k_2 = hf(t_n+c_2h, y_n+a_{21}k_1), \,

k_3 = hf(t_n+c_3h, y_n+a_{31}k_1+a_{32}k_2), \,

\vdots

k_s = hf(t_n+c_sh, y_n+a_{s1}k_1+a_{s2}k_2+\cdots+a_{s,s-1}k_{s-1}).

such that

s is the number of stages,

a_ij (for 1 ≤ j < i ≤ s),

b_i (for i = 1, 2, ..., s)

and c_i (for i = 2, 3, ..., s).

Example:finding the stability polynomial for RK4's methods

for RK4" case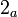 $2_a$ ", which characterizes by 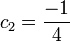$c_2= \frac {-1}{4}$ which has the form: the stability region is found by applying the method to the linear test equation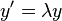 $y'=\lambda y$

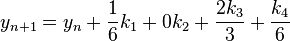
y_{n+1} = y_n + \frac{1}{6}k_1+0k_2+\frac {2k_3}{3}+\frac {k_4}{6}

the stability region is found by applying the method to the linear test equation

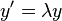
y'=\lambda y

\displaystyle \ k_1=hf(t_n,y_n)

k_2=hf(t_n+\frac{h}{2},y_n-\frac{k_1}{2})

k_3=hf(t_n+\frac{h}{2},y_n+\frac{3 k_1}{4}-\frac{ k_2}{4})

k_4=hf(t_n+h,y_n- 2k_1+k_2+2k_3)

using the linearized equation 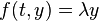$f(t,y)=\lambda y$ , we get

k_1=h\lambda y_n

k_2=h\lambda(1-\frac{h\lambda}{2})y_n

k_3=h\lambda(1+\frac{3 h\lambda}{4}-\frac { h \lambda}{4}(1-\frac{h\lambda}{2}))y_n

k_4=h\lambda(1-2h\lambda+ h\lambda(1-\frac{h\lambda}{2})+2h\lambda(1+\frac{3 h\lambda}{4}-\frac { h \lambda}{4}(1-\frac{h\lambda}{2})))))y_n

substitue these back in 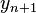$y_{n+1}$ , yields $y_{n+1} = [1+(h\lambda)+\frac{(h\lambda)^2}{2}+\frac{(h\lambda)^3}{6}+\frac{(h\lambda)^4}{24}]y_n=R(h\lambda)y_n$

and so the characteristic polynomial

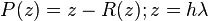$P(z)=z-R(z); z=h\lambda$ for the absolute stability region for this method, set |R(z)|<1, and so we get the region in figue1. case $2_a$

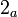
the table below shows the final forms for the stability function for different forms of RK4, these RK4's are different in the values of 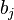$b_j$ , and they are fullfilling the consistencty requirement for the method i.e :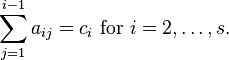 $\sum_{j=1}^{i-1} a_{ij} = c_i\ \mathrm{for}\ i=2, \ldots, s.$

case# 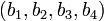$(b_1,b_2,b_3,b_4)$	stability function
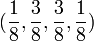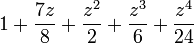caseI $(\frac{1}{8},\frac{3}{8},\frac{3}{8},\frac{1}{8})$	$1+\frac{7z}{8}+\frac{z^2}{2}+\frac{z^3}{6}+\frac{z^4}{24}$
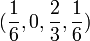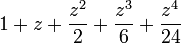caseII_a $(\frac{1}{6},0,\frac{2}{3},\frac{1}{6})$	$1+z+\frac{z^2}{2}+\frac{z^3}{6}+\frac{z^4}{24}$
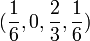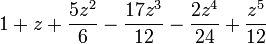caseII_b $(\frac{1}{6},0,\frac{2}{3},\frac{1}{6})$	$1+z+\frac{5z^2}{6}-\frac{17z^3}{12}-\frac{2z^4}{24}+\frac{z^5}{12}$
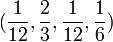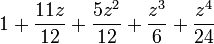caseIII $(\frac{1}{12},\frac{2}{3},\frac{1}{12},\frac{1}{6})$	$1+\frac{11z}{12}+\frac{5z^2}{12}+\frac{z^3}{6}+\frac{z^4}{24}$
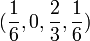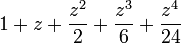caseIV $(\frac{1}{6},0,\frac{2}{3},\frac{1}{6})$	$1+z+\frac{z^2}{2}+\frac{z^3}{6}+\frac{z^4}{24}$
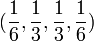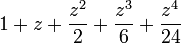classical Rk $(\frac{1}{6},\frac{1}{3},\frac{1}{3},\frac{1}{6})$	$1+z+\frac{z^2}{2}+\frac{z^3}{6}+\frac{z^4}{24}$

see to find the table

Plotting the stability region

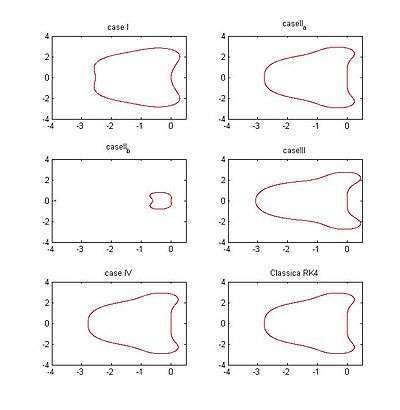
In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in the complex plane. Since R(z) is the unit circle in the complex plane, each point on the boundary can be represented as 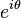$e^{i \theta}$ and so by changing 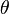$\theta$ over the interval $[0,2\pi]$ , we can draw the boundaries of that region. The following w:OCTAVE/Matlab code does this by plotting contour curves until reaching the boudaries:

[x,y] = meshgrid(-6:0.01:6,-6:0.01:6);
z = x+i*y;
R = 1+z+0.5*z^2+(1/6)*z^3+(1/24)*z^4;
zlevel = abs(R);
contour(x,y,zlevel,[1 1]);

The figure at right shows the absolute stability regions for RK4 cases which is tabulated above

References

Eberly, David (2008), stability analysis for systems of defferential equation .
Ababneh, Osama; Ahmad, Rokiah; Ismail, Eddie (2009), "on cases of fourth-order Runge-Kutta methods", European journal of scientific Research .
Mathews, John; Fink, Kurtis (1992), numerical methods using matlab .
Stability of Runge-Kutta Methods

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.