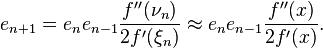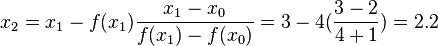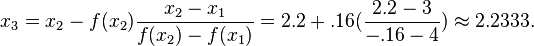Numerical Analysis/The Secant Method
< Numerical AnalysisThe Secant Method
The secant method is an algorithm used to approximate the roots of a given function f. The method is based on approximating f using secant lines.
The Algorithm
The secant method algorithm requires the selection of two initial approximations x 0 and x 1, which may or may not bracket the desired root, but which are chosen reasonably close to the exact root.
| Secant Method Algorithm |
|---|
| Given f(x)=0:
Let x0 and x 1 be initial approximations. Then 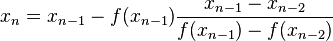 where xn is a better approximation of the exact root, assuming convergence. Repeat iterative step until either
|
Order of Convergence
We would like to be able to find the order of convergence, p, for the secant method. Hence, we want to find some p so that 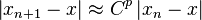 where C is a constant.
where C is a constant.
Given a function f, let x be such that f(x)=0 and let xn-1 and xn be approximations to x. Assume x is a simple root and f is twice continuously differentiable (from the assumptions leading to convergence noted on Wikipedia). Let the error at the nth step be denoted by en: en=xn-x. Then we have:
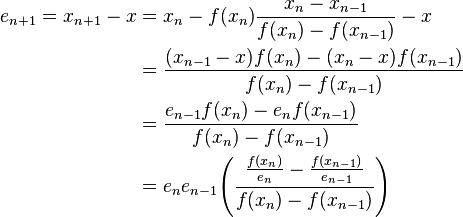 .
.
Since f(x)=0 and recalling that en=xn-x, we can rewrite the last line above as:
-
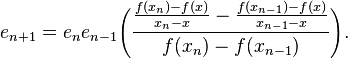
(1 )
Next, let's just consider the numerator in (1
).
Let 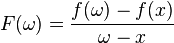 where
where 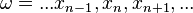 . Thus
. Thus
-
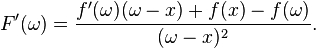
(2 )
According to the Mean Value Theorem, on [xn-1,xn], there exists some 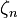 between xn-1 and xn such that
between xn-1 and xn such that 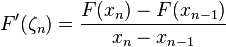
-
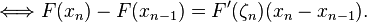
(3 )
Now using a Taylor expansion of  around
around 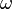 , we have
, we have
-
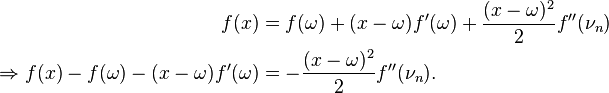
(4 )
Next, we can combine equations (2
), (3
), and (4
) to show that 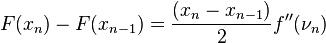 .
.
Returning to (1 ), we now have:
-
![e_{n+1}=e_ne_{n-1}\Bigg(\frac{F(x_n)-F(x_{n-1})}{f(x_n)-f(x_{n-1})}\Bigg)=\frac{e_ne_{n-1}(x_n-x_{n-1})}{2[f(x_n)-f(x_{n-1})]}f''(\nu_n).](../I/m/50a28fde6f54ec860f10d36a28b0a3c7.png)
(5 )
Again applying the Mean Value Theorem, there exists some 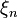 in [xn-1,xn] such that
in [xn-1,xn] such that 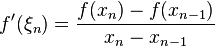 . Then (5
) becomes:
. Then (5
) becomes:
Next, recall that we have convergence of order p when 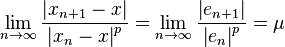 for some constant
for some constant 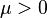 . Our goal is to figure out what p is for the secant method.
. Our goal is to figure out what p is for the secant method.
Let 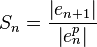
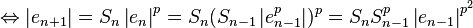 .
.
Then we have:
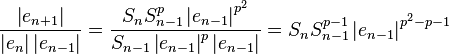 .
.
We want 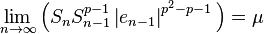 , again where
, again where 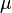 is some constant. Since
is some constant. Since 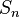 and
and 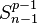 are constants and
are constants and 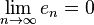 (assuming convergence) we must have
(assuming convergence) we must have 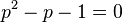 . Thus
. Thus 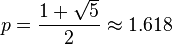 .[1]
.[1]
A Numerical Example
The function 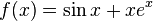 has a root between -3 and -4. Let's approximate this root accurate to four decimal places.
has a root between -3 and -4. Let's approximate this root accurate to four decimal places.
Let x0 = -3 and x1 = -4.
Next, using our recurrence formula where
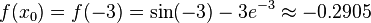
and
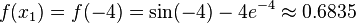 ,
,
we have:
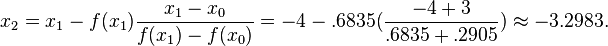
In the next iteration, we use f(x1) = .6835 and f(x2) = .0342 and see that
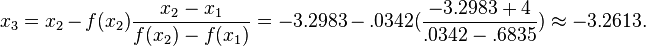
Similarly, we can compute x4 and x5. These calculations have been organized in the table below:
 | 0 | 1 | 2 | 3 | 4 | 5 |
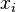 | -3 | -4 | -3.2983 | -3.2613 | -3.2665 | -3.2665 |
Hence the iterative method converges to -3.2665 after 4 iterations.
Pseudo Code
Below is pseudo code that will perform iterations of the secant method on a given function f.
Input: x0 and x1
Set y0=f(x0) and y1=f(x1)
Do
x=x1-y1*(x1-x0)/(y1-y0)
y=f(x)
Set x0=x1 and x1=x
Set y0=y1 and y1=y
Until |y1|<tol
Exercises
Exercise 1
Find an approximation to 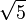 correct to four decimal places using the secant method on
correct to four decimal places using the secant method on 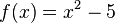 .
.
Solution:
We know 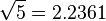 .
.
Let x0 = 2 and x1 = 3. Then f(x0) = f(2) = -1 and f(x1) = f(3) = 4.
In our first iteration, we have:
In the second iteration, f(x1) = 4, f(x2) = -0.16 and we thus have
Similarly, x3 and x4 can be calculated, and are shown in the table below:
 | 0 | 1 | 2 | 3 | 4 | 5 |
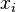 | 2 | 3 | 2.2 | 2.2333 | 2.2361 | 2.2361 |
Thus after 4 iterations, the secant method converges to 2.2361, an approximation to 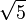 correct to four decimal places.
correct to four decimal places.
Exercise 2
Find a root of 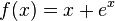 by performing five iterations of the secant method beginning with x0 = -1 and x1 = 0.
by performing five iterations of the secant method beginning with x0 = -1 and x1 = 0.
Solution:
1st Iteration: x0 = -1, x1 = 0, f(x0) = -0.63212, and f(x1) = 1. Then
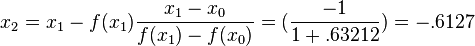
2nd Iteration: x1 = 0, x2 = -.6127, f(x1) = 1, and f(x2) = -.07081. Then
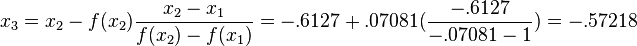
3rd Iteration: x2 = -.6127, x3 = -.57218, f(x2) = -.07081, and f(x3) = -.00789. Then
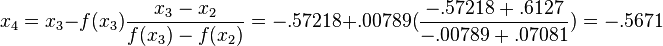
4th Iteration: x3 = -.57218, x4 = -.5671, f(x3) = -.00789, and f(x4) = 6.7843*10-5. Then
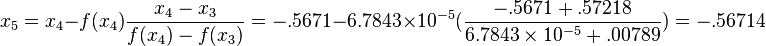
5th Iteration: x4 = -.5671, x5 = -.56714, f(x4) = 6.7843*10-5, and f(x5) = 5.1565*10-6. Then
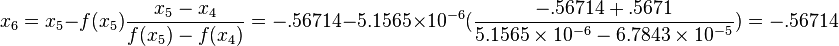
Thus after 5 iterations, the method converges to -.56714 as one of the roots of 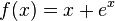 .
.
Quiz
The following is a quiz covering information presented on the associated secant method page on Wikipedia as well as the current page.
 , is achieved.
, is achieved.