Numerical Analysis/Romberg's method

< Numerical Analysis

Romberg's method approximates a definite integral by applying Richardson extrapolation to the results of either the trapezoid rule or the midpoint rule.

The initial approximations 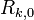$R_{k,0}$ are obtained by applying either the trapezoid or midpoint rule with 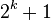$2^k + 1$ points. In the case of the trapezoid rule on $\left[a,b\right]$ ,

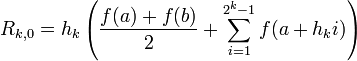
$R_{k,0} = h_k \left(\frac{f(a) + f(b)}{2} + \sum_{i=1}^{2^k - 1} f(a + h_k i)\right)$

where

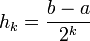
$h_{k} = \frac{b-a}{2^k}$

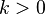For $k > 0$ , we can reduce the number of places the function is evaluated by using our previously obtained approximations instead of re-sampling. For the trapezoid rule, this improvement gives

$R_{0,0} = \left(\frac{b-a}{2}\right)[f(a)+f(b)]$

and

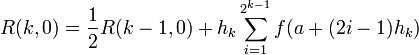
$R(k,0) = \frac{1}{2} R(k-1,0) + h_k \sum_{i=1}^{2^{k-1}} f(a + (2i-1)h_k)$

Richardson's extrapolation is then applied recursively, giving

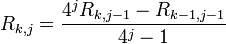
$R_{k,j} = \frac{4^j R_{k,j-1}-R_{k-1,j-1}}{4^{j}-1}$

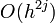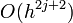Each successive level of improvement increases the order of error term from $O(h^{2j})$ to $O(h^{2j+2})$ at the expense of doubling the number of places the function is evaluated.

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.