Numerical Analysis/ODE in vector form Exercises
< Numerical AnalysisAll of the standard methods for solving ordinary differential equations are intended for first order equations. When you need to solve a higher order differential equation, you first convert it to a system of first order of equations. Then you rewrite as a vector form and solve this ODE using a standard method. On this page we demonstrate how to convert to a system of equations and then apply standard methods in vector form.
Reduction to a first order system
(Based on Reduction of Order and Converting a general higher order equation.)
I want to show how to convert higher order differential equation to a system of the first order differential equation. Any differential equation of order n of the form
can be written as a system of n first-order differential equations by defining a new family of unknown functions
The n-dimensional system of first-order coupled differential equations is then
Differentiating both sides yields
We can express this more compactly in vector form
where 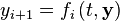 for
for 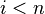 and
and 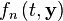 =
= 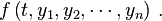
Exercise
Consider the second order differential equation 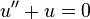 with initial conditions
with initial conditions 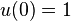 and
and 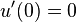 .
We will use two steps with step size
.
We will use two steps with step size 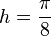 and approximate the values of
and approximate the values of 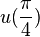 and
and 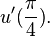
Since the exact solution is 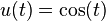 we have
we have 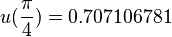 and
and 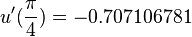 .
.
Exercise 1: Convert this second order differential equation to a system of first order equations.
Solution:
We have second order differential equation 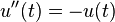 with initial conditions
with initial conditions 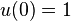 and
and 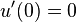 .
.
Let 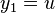 and
and 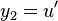 .
Differentiating
.
Differentiating 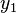 and
and 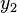 gives
gives
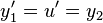 ,
, 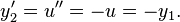
Thus we have a system of first order equation in vector form
Exercise 2: Apply the Euler method twice.
Solution:
By the Euler's method, 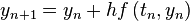 .
.
I. First apply to get 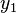
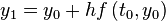 .
.
Now we convert 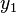 as a vector form, where
as a vector form, where 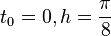 and
and
![\left[\begin{array}{c}
y_{0,1} \\ y_{o,2}
\end{array}\right]
= \left[\begin{array}{c}
1 \\ 0
\end{array} \right]](../I/m/cac875495b2376d1cab297d4d4b493d1.png) , then we have
, then we have
2. Second apply to get 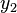
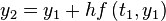 .
.
Similarly, we convert 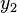 as a vector form, where
as a vector form, where 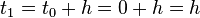 , where
, where 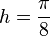 and
and ![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
= \left[\begin{array}{c}
1 \\ -h
\end{array} \right]](../I/m/5a0738c788f7b07ddcf57b5fc26f5fb7.png) , then we have
, then we have
Exercise 3: Apply the Backward Euler method twice.
Solution:
By the Backward Euler's method,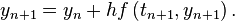
I. First apply to get 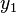
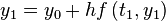 .
.
Now we convert 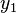 as a vector form, where
as a vector form, where 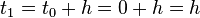 , where
, where 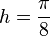 and
and
![\left[\begin{array}{c}
y_{0,1} \\ y_{o,2}
\end{array}\right]
= \left[\begin{array}{c}
1 \\ 0
\end{array} \right]](../I/m/cac875495b2376d1cab297d4d4b493d1.png) , then we have
, then we have
Now we have to solve a system of linear equations
That is,
Set up augmented matrix to solve this system,
Thus, the solution is 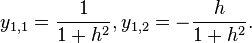
Plugging in 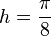 , then we have
, then we have
2. Second apply to get 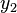
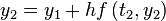 .
.
Similarly, we convert 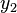 as a vector form, with
as a vector form, with 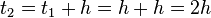 , where
, where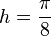 and
and ![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
= \left[\begin{array}{c}
{\frac{1}{1+h^2}} \\ {-\frac{h}{1+h^2} }
\end{array} \right]](../I/m/50239f4548b6bb4c9c64859221346baf.png) , then we have
, then we have
Now we have to solve a system of linear equations
That is,
Set up augmented matrix to solve this system,
Thus, the solution is 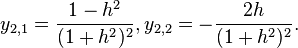
Plugging in 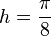 , then we have
, then we have
Exercise 4: Apply the Midpoint method twice.
Solution:
By the Midpoint method, 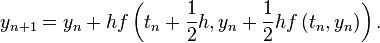
I. First apply to get 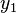
Now we convert 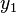 as a vector form, where
as a vector form, where 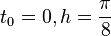 and
and ![\left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array}\right]
= \left[\begin{array}{c}
1 \\ 0
\end{array} \right]](../I/m/331d09edbbd14198b47e9391289b9d34.png) , then we have
, then we have
Plugging in 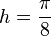 , then we have
, then we have
2. Second apply to get 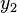
Now we convert 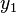 as a vector form, where
as a vector form, where 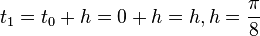 and
and ![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
= \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right]](../I/m/d10dccda6b20134a1cee0adb890e1491.png) , then we have
, then we have
Plugging in 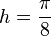 , then we have
, then we have
Exercise 5: Using the values from the Midpoint method at 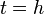 in exercise3, apply the Two-step Adams-Bashforth method once.
in exercise3, apply the Two-step Adams-Bashforth method once.
Solution:
By the Midpoint method, we found
Now apply the Two-step Adams-Bashforth method when 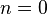 , then by formula
, then by formula
Vector form is following by
Plugging in 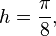
Reference
http://en.wikipedia.org/wiki/Ordinary_differential_equation
http://www.math.ohiou.edu/courses/math3600/lecture29.pdf
http://www.ohio.edu/people/mohlenka/20131/4600-5600/hw7.pdf
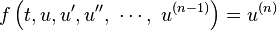
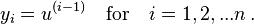
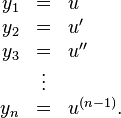
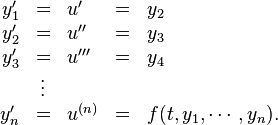
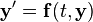
![\left[\begin{array}{c}
y_1' \\ y_2'
\end{array}\right]
= \left[\begin{array}{c}
y_2 \\ -y_1
\end{array} \right]
= f\left(t, \left[\begin{array}{c}
y_1 \\ y_2
\end{array} \right] \right)](../I/m/25692522b832c2da0441559b012d8160.png)
![\begin{align}
\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
& = \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h f\left(t_0, \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h\left[\begin{array}{c}
y_{0,2} \\ -y_{0,1}
\end{array}\right]
\\
& = \left[\begin{array}{c}
1 \\ 0
\end{array} \right]
+ h \left[\begin{array}{c}
0 \\ -1
\end{array}\right]
\\
& = \left[\begin{array}{c}
{1+0} \\{ 0-h}
\end{array} \right]
\\
& = \left[\begin{array}{c}
1 \\ {-h}
\end{array} \right]
\\
& = \left[\begin{array}{c}
1 \\ {- \frac{\pi}{8}}
\end{array} \right]
\\
& = \left[\begin{array}{c}
1 \\ {-0.392699082}
\end{array} \right]\,. \end{align}](../I/m/eed334572b25f0bb6d92a1b911a63d84.png)
![\begin{align}
\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]
& = \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ h f\left(t_1, \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ h\left[\begin{array}{c}
y_{2,1} \\ -y_{1,1}
\end{array}\right]
\\
& = \left[\begin{array}{c}
1 \\ {-h}
\end{array} \right]
+ h \left[\begin{array}{c}
{ -h} \\ { -1}
\end{array}\right]
\\
& = \left[\begin{array}{c}
{1-h^2} \\{ -h-h}
\end{array} \right]
\\
& = \left[\begin{array}{c}
{1-h^2} \\ -2h
\end{array} \right]
\\
& = \left[\begin{array}{c}
{1 - \frac{\pi^2}{8^2}}\\ {- 2 \frac{\pi}{8}}
\end{array} \right]
\\
& = \left[\begin{array}{c}
0.8457874321 \\ {-0.785398163}
\end{array} \right]\,.
\end{align}](../I/m/2d1a9b6cb781791a966dfb828d6a61e7.png)
![\begin{align}
\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
& = \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h f\left(t_1, \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h\left[\begin{array}{c}
y_{1,2} \\ -y_{1,1}
\end{array}\right]
\\
& = \left[\begin{array}{c}
1 \\ 0
\end{array} \right]
+ \left[\begin{array}{c}
{hy_{1,2}} \\ { -hy_{1,1}}
\end{array}\right]
\\
& = \left[\begin{array}{c}
{1+ hy_{1,2} } \\ { -hy_{1,1} }
\end{array} \right]\,.
\end{align}](../I/m/3538fec45fad0cd4051ce8a71d55443a.png)
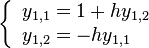

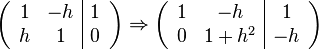
![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right] = \left[\begin{array}{c}
0.8457874321 \\ {-0.785398163}
\end{array} \right]\,.](../I/m/f05bc8e445e4fe992d4249d0b871da82.png)
![\begin{align}
\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]
& = \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ h f\left(t_2, \left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
{\frac{1}{1+h^2}} \\ {-\frac{h}{1+h^2}}
\end{array} \right]
+ h f \left(2h, \left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
{\frac{1}{1+h^2}} \\ {-\frac{h}{1+h^2}}
\end{array} \right]
+ h \left[\begin{array}{c}
y_{2,2} \\ {- y_{2,1} }
\end{array}\right]
\\
& = \left[\begin{array}{c}
{\frac{1}{1+h^2} + hy_{2,2} } \\ {-\frac{h}{1+h^2} - hy_{2,1} }
\end{array} \right]\,.
\end{align}](../I/m/90c033c9afc9cc02b555683fc8482c29.png)
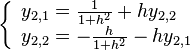
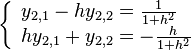
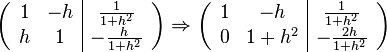
![\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right] = \left[\begin{array}{c}
0.63487705 \\ {-0.589546795}
\end{array} \right]\,.](../I/m/c41723eacaf73a0984aa035229ce21e0.png)
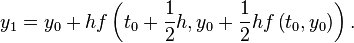
![\begin{align}
\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
&= \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h f\left(t_0 +\frac{1}{2} h , \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right] + \frac{1}{2} h f\left(t_0, \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right] \right)\right)
\\
&= \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right]
+ h f\left(t_0 +\frac{1}{2} h , \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array} \right] + \frac{1}{2} h \left[\begin{array}{c}
y_{0,2} \\ {-y_{0,1}}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
1 \\ 0
\end{array} \right]
+ h f\left(0 +\frac{1}{2} h , \left[\begin{array}{c}
1 \\ 0
\end{array} \right] + \frac{1}{2} h \left[\begin{array}{c}
0 \\ {-1}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
1 \\ 0
\end{array} \right]
+ h \left[\begin{array}{c}
{-\frac{1}{2} h} \\ {-1}
\end{array} \right]
\\
&= \left[\begin{array}{c}
{ 1 -\frac{1}{2} h^2}\\{-h}
\end{array} \right]\,.
\end{align}](../I/m/270f60daba1dc28bb31ff346671951f9.png)
![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right] = \left[\begin{array}{c}
0.922893716 \\ {-0.392699082}
\end{array} \right]\,.](../I/m/6d967b008aea18e3f123837f5ccfd32f.png)
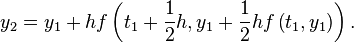
![\begin{align}
\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]
&= \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ h f\left(t_1 +\frac{1}{2} h , \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right] + \frac{1}{2} h f\left(t_1, \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right] \right)\right)
\\
&= \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ h f\left(h +\frac{1}{2} h , \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right] + \frac{1}{2} h \left[\begin{array}{c}
y_{1,2} \\ {-y_{1,1}}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right]
+ h f\left(\frac{3}{2} h , \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right] + \frac{1}{2} h \left[\begin{array}{c}
{-h} \\ {-1+\frac{1}{2}h^2}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right]
+ h f \left( \frac{3}{2} h , \left[\begin{array}{c}
{1- \frac{1}{2} h^2 - \frac{1}{2} h^2} \\ {-h- \frac{1}{2}h + \frac{1}{4}h^3}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right]
+ h f\left( \frac{3}{2} h , \left[\begin{array}{c}
{1- h^2} \\ {- \frac{2}{3}h+ \frac{1}{4} h^3}
\end{array} \right] \right)
\\
&= \left[\begin{array}{c}
{1- \frac{1}{2} h^2} \\ {-h}
\end{array} \right]
+ h \left[\begin{array}{c}
{- \frac{2}{3} h+ \frac{1}{4} h^3} \\ {-1+ h^2}
\end{array} \right]
\\
&= \left[\begin{array}{c}
{1-\frac{1}{2}h^2} \\ {-h}
\end{array} \right]
+ \left[\begin{array}{c}
{-\frac{2}{3}h^2+\frac{1}{4}h^4} \\ {-h+h^3}
\end{array} \right]
\\
&= \left[\begin{array}{c}
{1- \frac{1}{2}h^2- \frac{2}{3}h^2+ \frac{1}{4}h^4} \\ {-h-h+h^3}
\end{array} \right]
\\
&= \left[\begin{array}{c}
{1- 2h^2+ \frac{1}{4}h^4} \\ {-2h+h^3}
\end{array} \right]\,.
\end{align}](../I/m/e3c754cfd475f2e750862d7498d2219f.png)
![\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right] = \left[\begin{array}{c}
0.694547552011673 \\ {-0.7248390292562377}
\end{array} \right]\,.](../I/m/0e76f057288e17517f82a07504b2e4e8.png)
![\left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]
=\left[\begin{array}{c}
{1- \frac{1}{2}h^2} \\ {-h}
\end{array} \right]\,.](../I/m/dd79b0141fd6d06bbcf6339ef72373a3.png)
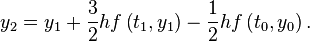
![\begin{align}
\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]
& = \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array} \right]
+ \frac{3}{2}h f \left(t_1, \left[\begin{array}{c}
y_{1,1} \\ y_{1,2}
\end{array}\right]\right)
- \frac{1}{2}h f \left( t_0, \left[\begin{array}{c}
y_{0,1} \\ y_{0,2}
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
{1- \frac{1}{2}h^2 }\\ {-h}
\end{array} \right]
+ \frac{3}{2}h f \left(t_1, \left[\begin{array}{c}
{1- \frac{1}{2}h^2 }\\ {-h}
\end{array}\right]\right)
- \frac{1}{2}h f \left( t_0, \left[\begin{array}{c}
1 \\ 0
\end{array}\right]\right)
\\
& = \left[\begin{array}{c}
{1- \frac{1}{2}h^2} \\ {-h}
\end{array} \right]
+ \frac{3}{2} h \left[\begin{array}{c}
{-h} \\ {-1+ \frac{1}{2}h^2}
\end{array}\right]
- \frac{1}{2}h \left[\begin{array}{c}
0 \\ {-1}
\end{array}\right]
\\
& = \left[\begin{array}{c}
{1-2h^2 } \\ {-2h+ \frac{3}{4}h^3 }
\end{array} \right]\,.
\end{align}](../I/m/ef56b63805dae787ce82a6912d26c875.png)
![\left[\begin{array}{c}
y_{2,1} \\ y_{2,2}
\end{array}\right]
= \left[\begin{array}{c}
0.691574862 \\ {-0.739978812}
\end{array} \right]\,.](../I/m/a3d2b279643b8dd718eaad6ca2d8f06d.png)