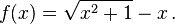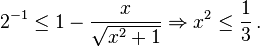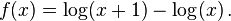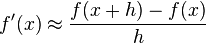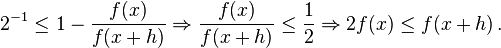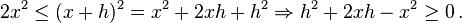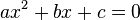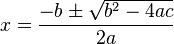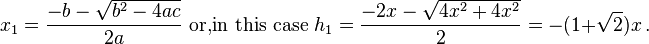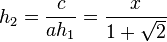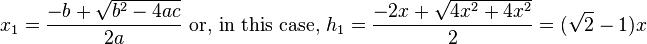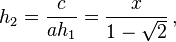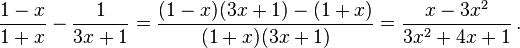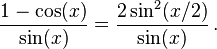Numerical Analysis/Loss of Significance

< Numerical Analysis

Loss of significance occurs in numerical calculations when too many significant digits cancel. As a result of the floating point arithmetic used by computers, when a number is subtracted from another number that is almost exactly the same, catastrophic cancellation may occur and an erroneous value returned. As an example, consider the behavior of

f(x)=\sqrt{x^2+1}-1

as x approaches 0. Evaluating this function at 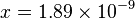$x=1.89\times 10^{-9}$ using Matlab incorrectly returns the answer 0, which shows that too many significant digits have cancelled.

If x and y are positive, normalized floating point binary numbers such that $x>y$ and

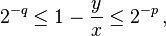
$2^{-q}\le1-{y\over x}\le2^{-p}\,,$

(bound )

then at most 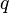$q$ and at least 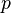$p$ significant binary bits are lost in the subtraction $x-y$ .

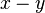On this page we will consider several exercises/examples of using this formula and show how sometimes we can rearrange the calculation to reduce loss of significance. Please try the exercise yourself before revealing the solution.

Exercises

Exercise 1

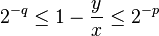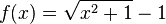Use $2^{-q}\le1-{y\over x}\le2^{-p}$ to find a lower bound on the input x if one desires to lose no more than 1 significant binary bit in the calculation of $f(x)=\sqrt{x^2+1}-1$ .

Solution:

In (bound ), "x" is 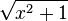$\sqrt{x^2 + 1}$ and "y" is 1; "q" = 1. We have 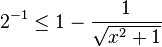$2^{-1}\le 1-{1\over\sqrt{x^2 +1}}$ . Solving for x, we have 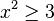$x^2\ge3$ , which is our lower bound on x.

Exercise 2

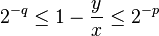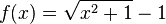Use $2^{-q}\le1-{y\over x}\le2^{-p}$ to find a lower bound on the input x if one desires to lose at most 3 significant binary bits in the calculation of $f(x)=\sqrt{x^2+1}-1$ .

Solution:

In (bound ), "x" is 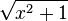$\sqrt{x^2 + 1}$ and "y" is 1; "q" = 3. We have 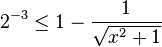$2^{-3}\le 1-{1\over\sqrt{x^2 +1}}$ . Solving for x, we have 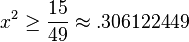$x^2\ge{15\over 49}\approx.306122449$ , which is our lower bound on x.

Exercise 3

Consider

f(x)=\sqrt{x^{2}+1}-x\,.

As x gets very large, loss of significance can occur. What is the bound on x if we want to lose no more than one binary digit?

Solution:

We have

2^{-1}\le 1-{x\over \sqrt{x^{2}+1}}\Rightarrow x^{2}\le {1\over 3}\,.

Exercise 4

Now consider the function

f(x)=\log(x+1)-\log(x)\,.

For large values of x, loss of significance may occur.

Use (bound ) to find a bound on the input so that at most 1 significant binary bit will be lost in the calculation.

Solution:

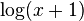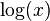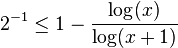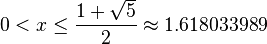In (bound ), "x" is $\log(x+1)$ , "y" is $\log(x)$ , and "q" is 1. We have $2^{-1}\le 1-{\log(x)\over \log(x+1)}$ . Solving for x gives the interval $0 < x \le {1+\sqrt{5}\over 2}\approx1.618033989$ .

Exercise 5

In w:Numerical differentiation, the w:Finite difference

f'(x)\approx{f(x+h)-f(x)\over h}

is often used to approximate derivatives. w:Truncation error can be reduced by decreasing "h", the step size, but if h becomes too small, loss of significance can become a factor. For 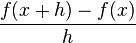${f(x+h)-f(x)\over h}$ , find a bound on h such that at most 1 binary bit will be lost in the calculation.

Solution:

We have

2^{-1}\le 1-{f(x)\over f(x+h)} \Rightarrow {f(x)\over f(x+h)}\le {1\over2} \Rightarrow 2f(x)\le f(x+h)\,.

Exercise 6

For 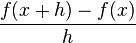${f(x+h)-f(x)\over h}$ , find a bound on h such that at most 1 binary bit will be lost in the calculation, if $f(x)=x^{2}$ .

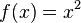Solution:

We have

2x^{2}\le (x+h)^{2}=x^{2}+2xh+h^{2} \Rightarrow h^{2}+2xh-x^{2}\ge 0\,.

Comparing this equation to the general form,

ax^{2}+bx+c=0

and using the w:quadratic formula

x={-b\pm\sqrt{b^{2}-4ac}\over2a}

we see that the variable in our equation is "h", a = 1, b = 2x, and c = x^2. We use the quadratic formula to solve for "h".

The quadratic formula itself can be a cause of w:loss of significance if the quantity "4ac" is very small. This can be remedied by not subtracting.

If "b" (in this case, "2x") is positive, subtraction can be avoided by using

x_1={-b-\sqrt{b^{2}-4ac}\over2a}\text{ or,in this case }h_1={-2x-\sqrt{4x^{2}+4x^{2}}\over2}=-(1+\sqrt{2})x\,.

Unfortunately, this gives a value for "h" that is always negative, which is unacceptable. Using one of w:Vieta's formulas,

h_2={c\over ah_1}={x\over 1+\sqrt{2}}

which gives positive values for h. If "b" (here, "2x") is negative, we use

x_1={-b+\sqrt{b^{2}-4ac}\over2a}\text{ or, in this case, } h_1={-2x+\sqrt{4x^{2}+4x^{2}}\over2}=(\sqrt{2}-1)x

which, again, always gives a negative value for h. However, Vieta's formula gives

h_2={c\over ah_1}={x\over1-\sqrt{2}}\,,

which returns positive values for h. The bounds on h are then:

Failed to parse (unknown function "\tex"): h\ge {x\over 1+\sqrt{2}}\quad \text{for } x > 0\quad\tex{and}

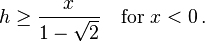
h\ge {x\over 1-\sqrt{2}}\quad \text{for } x < 0\,.

Exercise 7

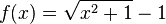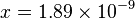Rewrite $f(x)=\sqrt{x^2+1}-1$ so that there is no loss of significance, then evaluate it at $x=1.89\times 10^{-9}$ .

Solution:

Rationalize the expression:

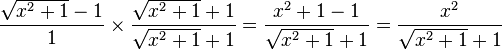{\sqrt{x^2 + 1}-1\over 1}\times {\sqrt{x^2 + 1}+1\over \sqrt{x^2 + 1}+1} = {x^2 + 1 - 1\over \sqrt{x^2 + 1}+1} = {x^2\over \sqrt{x^2 + 1}+1}

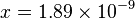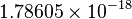Evaluating this expression at $x=1.89\times10^{-9}$ gives an answer of $1.78605\times 10^{-18}$ .

Exercise 8

Rewrite 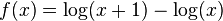$f(x)=\log(x+1)-\log(x)$ so that loss of significance will be minimized.

Solution:

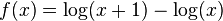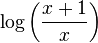Use the Quotient Property of logarithms to rewrite $f(x)=\log(x+1)-\log(x)$ as $\log\left({x+1\over x}\right)$ .

Exercise 9

For very small values of x, loss of significance can occur in 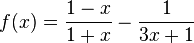$f(x)={1-x\over 1+x}-{1\over 3x+1}$ . Rewrite this function in a way that will minimize loss of significance.

Solution:

Giving both terms a common denominator and combining them into a single rational expression reduces loss of significance. We then have

{1-x\over1+x}-{1\over3x+1}={(1-x)(3x+1)-(1+x)\over(1+x)(3x+1)}={x-3x^{2}\over3x^{2}+4x+1}\,.

Exercise 10

As x gets close to zero, loss of significance can occur in 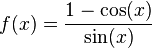$f(x)=\frac{1-\cos(x)}{\sin(x)}$ . Rewrite this function in a way that will minimize loss of significance.

Solution:

The loss of significance occurs in the numerator, so rewrite the numerator using a trigonometric identity to get

\frac{1-\cos(x)}{\sin(x)}=\frac{2\sin^{2}(x/2)}{\sin(x)}\,.

This article is issued from Wikiversity - version of the Saturday, April 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.