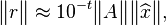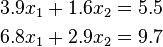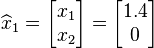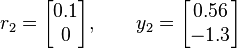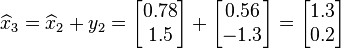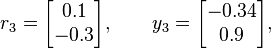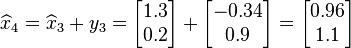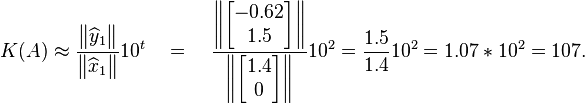Numerical Analysis/Iterative Refinement
< Numerical AnalysisWhat is Iterative Refinement?
A detailed discussion of iterative refinement can be found on the Wikipedia page.
To give a brief description, it is a technique used to improve the approximate solution 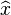 to linear system
to linear system 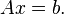 This technique is generally only used on systems that are thought or determined to be ill-conditioned.
This technique is generally only used on systems that are thought or determined to be ill-conditioned.
The process involves three primary steps:
| Iterative Refinement Process |
|---|
| Once an approximation to the solution,
Continue to update step one with the newly calculated |
Approximating the Condition Number
In theory, the condition number of a matrix depends on the norms of the matrix and its inverse. In practice, however, calculating the inverse is subject to round-off error and the accuracy of the calculations.
If these calculations involve arithmetic with t digits of accuracy, then the approximate condition number for the matrix - call it A - is the norm of A the norm of the approximation of the inverse of A.
Assuming that the approximate solution to the linear system is being determined with t-digit arithmetic and Gaussian elimination, we can show
where r is the residual vector for the approximation 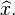
This approximation for the condition number can be obtained without having to invert matrix A.
When doing iterative refinement problems, we will have, or will calculate the values for 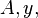 and
and 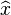 . The approximate solution,
. The approximate solution, 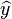 satisfies
satisfies
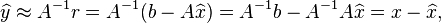
so 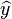 is an estimate of the error for approximate solution
is an estimate of the error for approximate solution 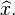 Observe that
Observe that
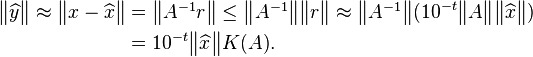
This approximates the condition number associated with solving 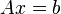 and can be re-written and expressed as seen here:
and can be re-written and expressed as seen here:
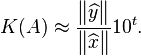 |
Example
Consider the following ill-conditioned linear system
Part 1
Solve using Gaussian elimination and iterative refinement (and using two-digit rounding arithmetic). Continue using iterative refinement until 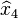 is found. Compare with the true solution.
is found. Compare with the true solution.
Solution:
First, use a calculator or computer to find the true solution 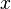 of this system. We will discover that
of this system. We will discover that
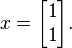
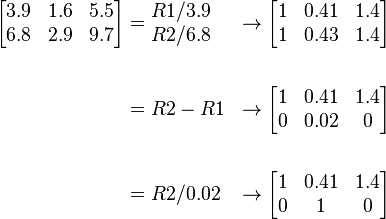
Set up the augmented matrix and solve using Guassian elimination, making sure to use only two-digit rounding arithmetic.
Solving with back-substitution we find the first approximation to the system:
Because we mentioned that this system is ill-conditioned, we can use the iterative refinement process to find a better approximation. Recall the steps mentioned above:
- Compute residual:
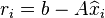
- Solve
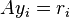
- Update
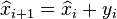
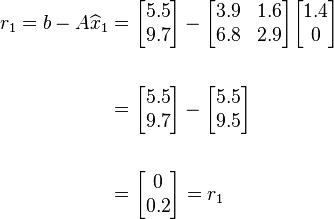
STEP 1: Compute the residual 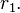
STEP 2: Now solve 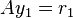 using rounded Gaussian elimination to find the
using rounded Gaussian elimination to find the 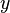 vector.
vector.
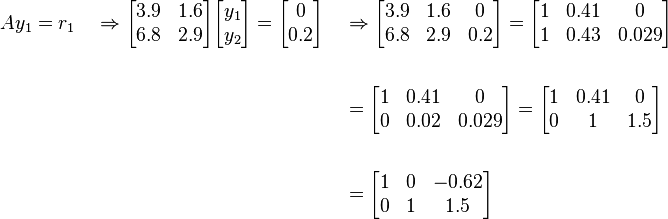
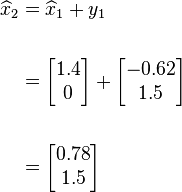
STEP 3: Update 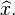
Note that 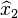 is a better representation of
is a better representation of 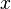 , than
, than 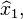 however it is still not a very accurate representation. Continue with a couple more iterations.
however it is still not a very accurate representation. Continue with a couple more iterations.
Repeat, as needed.
In the second iteration of Iterative Refinement, we find the following:
Thus,
In the third iteration we find
which we can use to find our final approximation, 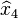 as
as
Recall that the true solution of the linear system is 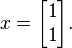 After completing three iterations of iterative refinement we have approximate the solution
After completing three iterations of iterative refinement we have approximate the solution 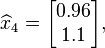 which is significantly closer than our original approximation
which is significantly closer than our original approximation 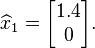
Part 2
Estimate the condition number 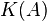 in Part 1 using the method discussed above, and compare this with the condition number calculated using norms.
in Part 1 using the method discussed above, and compare this with the condition number calculated using norms.
Solution:
We can find the true condition number by calculating it using norms - in the way it is described on the condition number Wikipedia . (Keep in mind, we will still use 2 significant digits in this example as well.)
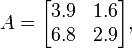 and
and 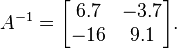
We can then solve for the condition number 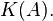
We can use our approximations, 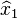 and
and 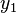 , found in the first iteration of Example 1 to use in the method we learned above, on Approximating the Condition Number.
, found in the first iteration of Example 1 to use in the method we learned above, on Approximating the Condition Number.
So we have found the true condition number to be 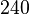 and the approximation to be
and the approximation to be 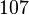 . These numbers are both in the realm of
. These numbers are both in the realm of 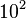 , meaning both for the true and approximate condition number, we can see there may be a loss of two digits of accuracy.
, meaning both for the true and approximate condition number, we can see there may be a loss of two digits of accuracy.
Quiz
References
Burden and Faires. Numerical Analysis, 3rd Edition. ISBN 0-87150-857-5
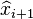 until a desired tolerance has been reached.
until a desired tolerance has been reached.