Numerical Analysis/Divided differences
< Numerical AnalysisThe Expanded Form of the Definition
The usual definition of divided differences is equivalent to the Expanded form
-
![f[x_0,x_1\dots,x_n] =\sum_{j=0}^{n} \frac{f(x_j)}{\prod_{k\in\{0,\dots,n\}\setminus\{j\}} (x_j-x_k)}](../I/m/104b3be7bdf332abbe83ff52c4fbe60b.png)
(expanded )
With help of a polynomial functions 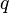 with
with 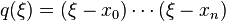 this can be written as
this can be written as
Since we will need the Expanded form (expanded ) for our other work below, we first prove that it is equivalent to the usual definition.
Proof of the expanded form
For 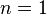 , (expanded
) holds because
, (expanded
) holds because
We now assume (expanded
) holds for  and show that this implies it also holds for
and show that this implies it also holds for 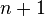 .
Thus by induction it holds for all
.
Thus by induction it holds for all  .
.
If the formula ![f[x_0,x_1,\ldots,x_n]=\sum_{j=0}^n\frac{f(x_j)}{q'(x_j)}](../I/m/e20eb4dcf3373973a982088a42e19b84.png) , where
, where 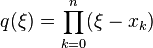 , then denoting
, then denoting 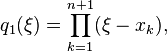
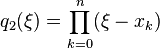 and
and 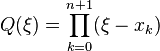 , we have
, we have
We have,
and
which gives
Hence, since the assertion hold for 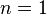 and
and 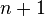 , then by induction, the assertion holds for all positive integer
, then by induction, the assertion holds for all positive integer  .
.
Symmetry property of divided differences
The divided differences have a number of special properties that can simplify work with them. One of the property is called the Symmetry Property which states that the Divided differences remain unaffected by permutations (rearrangement) of their variables.
Now we prove this symmetry property by showing that
When 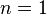 , we have
, we have
Hence ![f[x_1,x_0]=f[x_0,x_1]](../I/m/0fc6b4326dbbb8aea257fe9166caddad.png) , which is the symmetry of the first divided difference.
, which is the symmetry of the first divided difference.
When 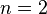 , we have
, we have
Hence ![f[x_2,x_1,x_0]=f[x_0,x_1,x_2]=f[x_1,x_0,x_2]](../I/m/936217537586c69846770a73f707fbe9.png) etc., which is the symmetry of the second divided difference.
etc., which is the symmetry of the second divided difference.
Similarly, when 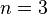 we have
we have
Hence ![f[x_3,x_2,x_1,x_0]=f[x_0,x_1,x_2,x_3]=f[x_1,x_0,x_3,x_2]](../I/m/0c8b94b6addc7d47103d5b807cbd0da7.png) etc., which is the symmetry of the third divided difference.
etc., which is the symmetry of the third divided difference.
In general, we can use the Expanded Form (expanded ) to obtain
Hence ![f[x_0,x_1\dots,x_n]=f[x_1,x_0\dots,x_n]](../I/m/0e6aee6b4703257fa7987f9bd7a0b302.png) etc., which is the symmetry of the
etc., which is the symmetry of the 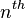 divided difference.
divided difference.
Computing the divided differences in tabular form
A difference table is again a convenient device for displaying differences, the standard diagonal form being used and thus the generation of the divided differences is outlined in Table below.
A Numerical Example 1
For a function  , the divided differences are given by
, the divided differences are given by
find ![f[x_0,x_1,x_2]](../I/m/80956a951d407558979b2ccb05bc0dde.png) .
.
Solution:
Hence, ![f[x_1,x_0,x_2]=-1](../I/m/e312a01b02a06151d3d06bfe42b3dab7.png) and by symmetry property we know that
and by symmetry property we know that ![f[x_1,x_0,x_2]=f[x_0,x_1,x_2]](../I/m/33a7a05a18d35b97edefef6b3523945b.png) , Hence
, Hence ![f[x_0,x_1,x_2]=-1](../I/m/a6ce8d36e4ac5a064d05c2a32172845a.png) .
.
A Numerical Example 2
For a function  , the divided differences are given by
, the divided differences are given by
Determine the missing entries in the table.
Solution:
We have the formula
and substituting gives
Thus,
Using the formula
and substituting gives
Thus,
Further,
So,
Thus,
![f[x_0]=3-2=1](../I/m/ce84a52399685fbee176a42052ac26f0.png) .
.
Algorithm: Computing the Divided Differences
Algorithm: Newton's Divided-Differences
Given the pointsStep 1: Initialize
Step 2: For
For
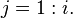
End End Result: The diagonal,
now contains
Relationship between Generalization of the Mean Value Theorem and the Derivatives
Generalization of the Mean Value Theorem
For any n + 1 pairwise distinct points x0, ..., xn in the domain of an n-times differentiable function f there exists an interior point
where the nth derivative of f equals  ! times the
! times the 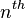 divided difference at these points:
divided difference at these points:
This is called the Generalized Mean Value Theorem.
For 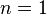 we have
we have
for some 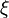 between
between 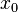 and
and  ,
which is exactly Mean Value Theorem.
We have extended MVT to higher order derivatives as
,
which is exactly Mean Value Theorem.
We have extended MVT to higher order derivatives as
What is the theorem telling us?
- This theorem is telling us that the Newton's
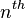 divided difference is in some sense approximation to the
divided difference is in some sense approximation to the 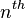 derivatives of
derivatives of  .
.
A Numerical Example
Let 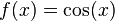 ,
, 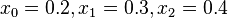 . Then, Show that
. Then, Show that
for some 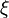 between the minimum and maximum of
between the minimum and maximum of 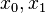 and
and 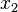 .
.
Solution:
If we chose 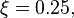 Where
Where 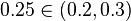 and we get
and we get 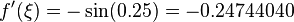 and we can see that
and we can see that ![f[x_0,x_1]](../I/m/5fb1effc4eb7fe9e9b3d249bdddcc43a.png) is a very good approximation of this derivative.
Similarly,
is a very good approximation of this derivative.
Similarly,
and
Thus, by the Generalized Mean Value Theorem with 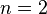 we have
we have
for some 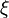 between the minimum and maximum of
between the minimum and maximum of 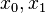 and
and 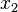 .
Taking
.
Taking 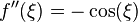 with
with 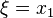 , we have
, we have 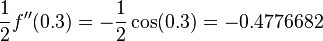 which is nearly equal to the result of
which is nearly equal to the result of ![f[x_0,x_1,x_2]=-0.4772705](../I/m/80a4d04af6b13ca6e83c607ef57d1d45.png) Thus with this example we conclude that the Newton's
Thus with this example we conclude that the Newton's 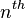 divided difference is in some sense an approximation to the
divided difference is in some sense an approximation to the 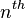 derivatives of
derivatives of  .
.
Quiz
Reference
- Guide to Numerical Analysis by Peter R. Turner
- Numerical Analysis by Richard L. Burden and J. Douglas Faires (EIGHT EDITION)
- Elementary Numerical Analysis by Kendall Atkinson (Second Edition)
- Applied Numerical Analysis by Gerald / Wheatley (Sixth Edition)
- Theory and Problems of Numerical Analysis by Francis Scheid
![f[x_0,\dots,x_n] = \sum_{j=0}^{n} \frac{f(x_j)}{q'(x_j)}\,.](../I/m/b32ae8d167d7ea4f81c6e53d35d87f89.png)
![f[x_0,x_1]= \frac{f[x_1]-f[x_0]}{x_1-x_0}= \frac{f(x_0)}{(x_0-x_1)} + \frac{f(x_1)}{(x_1-x_0)}\,.](../I/m/5ec7a3c6ca5fc7c08a9d5ab3c6720c69.png)
![\begin{align}
f[x_0,x_1,\ldots,x_{n+1}]&=\frac{f[x_1,\ldots,x_{n+1}]-f[x_0,\ldots,x_n]}{x_{n+1}-x_0}\\&=\frac 1{x_{n+1}-x_0}\left(\sum_{j=0}^n\frac{f(x_{j+1})}{q_1'(x_{j+1})}-\sum_{j=0}^n\frac{f(x_j)}{q_2'(x_j)}\right)\\&=\frac 1{x_{n+1}-x_0}\left(\sum_{k=1}^{n+1}\frac{f(x_k)}{q_1'(x_k)}-\sum_{k=0}^n\frac{f(x_k)}{q_2'(x_k)}\right)\\&=\frac 1{x_{n+1}-x_0}\left(\frac{f(x_{n+1})}{q_1'(x_{n+1})}+\sum_{k=1}^nf(x_k)\left(\frac 1{q_1'(x_k)}-\frac 1{q_2'(x_k)}\right)-\frac{f(x_0)}{q_2'(x_0)}\right)
\,.
\end{align}](../I/m/eee457bdc10764930dfd0fac72c2c748.png)
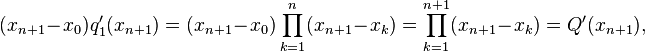
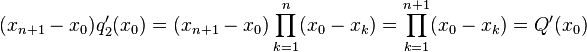
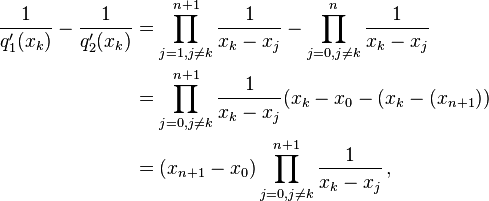
![f[x_0,x_1,\ldots,x_{n+1}]=\sum_{j=0}^{n+1}\frac{f(x_j)}{Q'(x_{j+1})}=\sum_{j=0}^{n+1} \frac{f(x_j)}{\prod_{k\in\{0,\dots,n\}\setminus\{j\}} (x_j-x_k)}\,.](../I/m/d2c5fe2531ef229312a8fa13cf2a9eea.png)
![f[x_0,x_1\dots,x_n]=f[x_1,x_0\dots,x_n]\quad \text{etc.}](../I/m/812532ac34743b0229c831fdef600ea5.png)
![f[x_1,x_0]= \frac{f[x_1]-f[x_0]}{x_1-x_0}= \frac{f(x_0)}{(x_0-x_1)} + \frac{f(x_1)}{(x_1-x_0)}= \frac{f[x_0]-f[x_1]}{x_0-x_1}=f[x_0,x_1]\,.](../I/m/ff4b0d7ece068df54aa381ba1a37f116.png)
![\begin{align}
f[x_2,x_1,x_0] &= \frac{f[x_2,x_1]-f[x_1,x_0]}{x_2-x_0}=\frac{{\frac{f[x_2]-f[x_1]}{x_2-x_1}}-{\frac{f[x_1]-f[x_0]}{x_1-x_0}}}{x_2-x_0}\\&=\frac{f(x_2)}{(x_2-x_0)\cdot(x_2-x_1)} + \frac{f(x_1)}{(x_1-x_0)\cdot(x_1-x_2)} + \frac{f(x_0)}{(x_0-x_1)\cdot(x_0-x_2)}\\&=f[x_0,x_1,x_2]=f[x_1,x_0,x_2]
\quad\text{etc.}
\end{align}](../I/m/98759dcae1130b4a83b1f070de02a78b.png)
![\begin{align}
f[x_3,x_2,x_1,x_0]&=\frac{f[x_3,x_2,x_1]-f[x_2,x_1,x_0]}{x_3-x_0}\\&=\frac{f(x_0)}{(x_0-x_1)\cdot(x_0-x_2)\cdot(x_0-x_3)} + \frac{f(x_1)}{(x_1-x_0)\cdot(x_1-x_2)\cdot(x_1-x_3)} + \frac{f(x_2)}{(x_2-x_0)\cdot(x_2-x_1)\cdot(x_2-x_3)} +\\&\quad\quad \frac{f(x_3)}{(x_3-x_0)\cdot(x_3-x_1)\cdot(x_3-x_2)}\\&=f[x_0,x_1,x_2,x_3]=f[x_1,x_0,x_2,x_3]\quad\text{etc.}
\end{align}](../I/m/cdb7d209468f0a0f606a314865ec4a19.png)
![f[x_0,x_1\dots,x_n] =\sum_{j=0}^{n} \frac{f(x_j)}{\prod_{k\in\{0,\dots,n\}\setminus\{j\}} (x_j-x_k)}= f[x_1,x_0\dots,x_n]\quad\text{etc.}](../I/m/8579122ccfc12f3c7be05e6a989bb3d2.png)
![\begin{matrix}
x & f(x) &\text{First Divided Difference} &\text{Second Divided Difference} &\text{Third Divided Difference} &\text{Fourth Divided Difference} \\
x_0 & f[x_0] & & & \\
& &f[x_0,x_1]= \frac{f[x_1]-f[x_0]}{x_1-x_0} & \\
x_1 & f[x_1]& &f[x_0,x_1,x_2]= \frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}& \\
& &f[x_1,x_2]= \frac{f[x_2]-f[x_1]}{x_2-x_1} & &f[x_0,x_1,x_2,x_3]= \frac{f[x_1,x_2,x_3]-f[x_0,x_1,x_2]}{x_3-x_0}\\
x_2 & f[x_2]& &f[x_1,x_2,x_3]= \frac{f[x_2,x_3]-f[x_1,x_2]}{x_3-x_1}& &f[x_0,x_1,x_2,x_3,x_4]=\frac{f[x_1,x_2,x_3,x_4]-f[x_0,x_1,x_2,x_3]}{x_4-x_0} \\
& &f[x_2,x_3]= \frac{f[x_3]-f[x_2]}{x_3-x_2} & &f[x_1,x_2,x_3,x_4]= \frac{f[x_2,x_3,x_4]-f[x_1,x_2,x_3]}{x_4-x_1}\\
x_3 & f[x_3]& &f[x_2,x_3,x_4]= \frac{f[x_3,x_4]-f[x_2,x_3]}{x_4-x_2}& \\
& &f[x_3,x_4]= \frac{f[x_4]-f[x_3]}{x_4-x_3}& \\
x_4 & f[x_4]& \\
\end{matrix}](../I/m/5fba6f3086917f79e64a19dbf969593c.png)
![\begin{matrix}
x_1=2& f[x_1]=2& \\
& \\
x_0=1& f[x_0]=-6& \\
& \\
x_2=4& f[x_2]=12& \\
\end{matrix}](../I/m/3e21abe63fb283d9595b6974d780da39.png)
![\begin{matrix}
x& f(x) &\text{First Divided Difference} &\text{Second Divided Difference} \\
x_1=2& f[x_1]=2& & \\
& &f[x_1,x_0]=\frac{(-6)-2}{1-2}=8& & \\
x_0=1& f[x_0]=-6& &f[x_1,x_0,x_2]=\frac{6-8}{4-2}=-1 \\
& &f[x_0,x_2]=\frac{12-(-6)}{4-1}=6& & \\
x_2=4& f[x_2]=12& & \\
\end{matrix}](../I/m/5d52cd9f4331f78f18230ad683fcb0bf.png)
![\begin{matrix}
x_0=0.0& f[x_0]& & \\
& &f[x_0,x_1]& & \\
x_1=0.4& f[x_1] & & &f[x_0,x_1,x_2]=\frac{50}{7}& \\
& &f[x_1,x_2]=10& & \\
x_2=0.7& f[x_2]=6& & \\
\end{matrix}](../I/m/5d8b43ec4d42a03bdb7f0683b0435664.png)
![f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}](../I/m/5baaf621be7521690959a80f9d80a871.png)
![\frac{50}{7}=\frac{(10-f[x_0,x_1])}{0.7}\,.](../I/m/c4af3856655bd50c6f6250824229f597.png)
![f[x_0,x_1]=-0.7\cdot(\frac{50}{7}) + {10}=5](../I/m/9813e419825d0b3a8967e916afb93ec3.png)
![f[x_1,x_2]=\frac{f[x_2]-f[x_1]}{x_2-x_1}](../I/m/90b4a5cdadbadf82fad1fc3408f6f84e.png)
![10=\frac{(6-f[x_1])}{0.3}\,.](../I/m/4c90cb2d41a18f841d858519662722c0.png)
![f[x_1]=6-3=3\,.](../I/m/757c4e926bed437e0394599c9004fcb6.png)
![f[x_0,x_1]= \frac{f[x_1]-f[x_0]}{x_1-x_0}\,.](../I/m/0d4fd9f76c063e62aa0bf5713c97d2fc.png)
![5=\frac{(3-f[x_0])}{0.4}\,.](../I/m/4035aeb88ac6a64d9ef607f97a484b49.png)
![f[x_0,...,x_i].](../I/m/aaba6020bb7b008c698e74bebac05703.png)
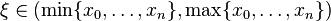
![f[x_0,\dots,x_n] = \frac{f^{(n)}(\xi)}{n!}\,.](../I/m/2208c97072249ade4bbabf6cc2f55591.png)
![f[x_0,x_1]= \frac{f[x_1]-f[x_0]}{x_1-x_0}=f'(\xi)](../I/m/81fba46048d6a35ef322027654d2ac58.png)
![f[x_0,x_1]\approx f'(\xi)](../I/m/a9053a1f22776046f86fd27066a09f1e.png)
![f[x_0,x_1,x_2]\approx\frac{1}{2}f''(\xi)](../I/m/ab452963932b2d8ee459c566d34ba918.png)
![f[x_0,x_1]= \frac{f[x_1]-f[x_0]}{x_1-x_0}=\frac{\cos(0.3)-\cos(0.2)}{0.3-0.2}=-0.2473009](../I/m/5eb84320a2bd9048040ccc8a70c35608.png)
![f[x_1,x_2]= \frac{f[x_2]-f[x_1]}{x_2-x_1}=\frac{\cos(0.4)-\cos(0.3)}{0.4-0.3}=-0.3427550](../I/m/f1e1855fbe4f0e8dcb3909a780511e8e.png)
![f[x_0,x_1,x_2]= \frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}=\frac{-0.3427550-(-0.2473009)}{0.4-0.2}=-0.4772705\,.](../I/m/57d375456433a32daf1ec36af4c11750.png)
![f[x_0,x_1,x_2]=\frac{1}{2}f''(\xi)](../I/m/5cf63a716884cd6a7857e42be78cb0cd.png)