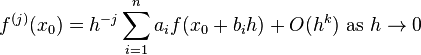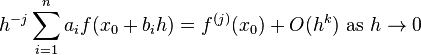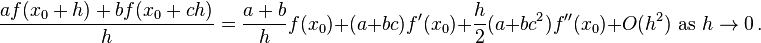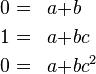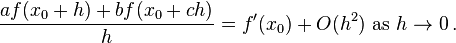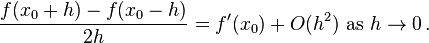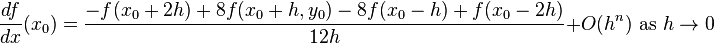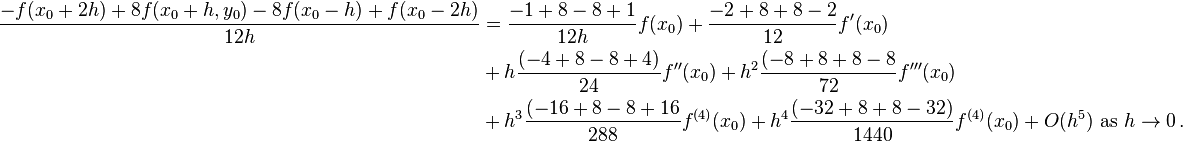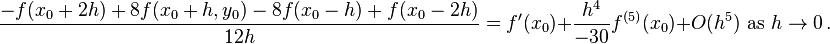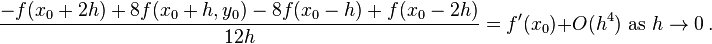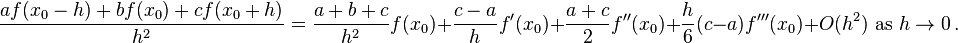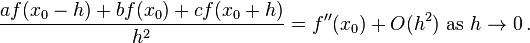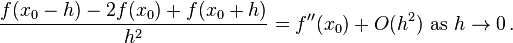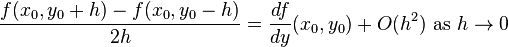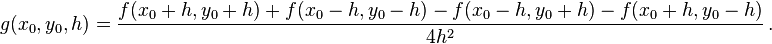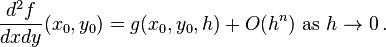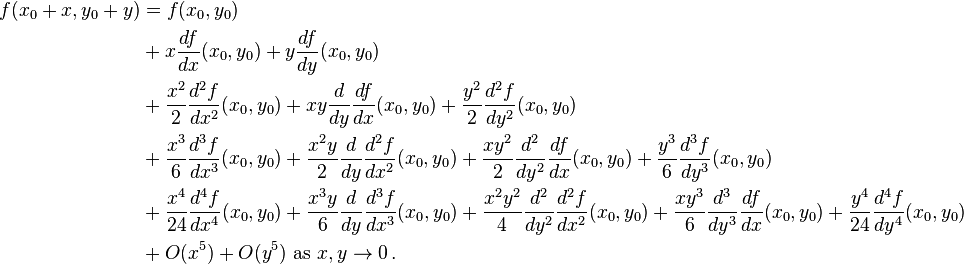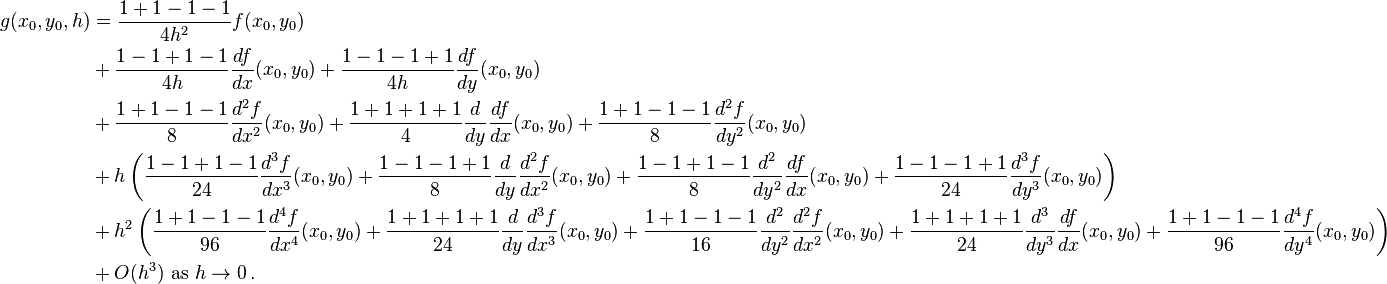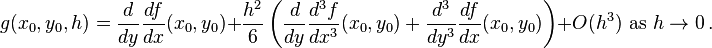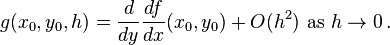Numerical Analysis/Differentiation/Examples
< Numerical Analysis < DifferentiationWhen deriving a finite difference approximation of the 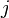 th derivative of a function
th derivative of a function 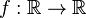 , we wish to find
, we wish to find 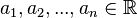 and
and 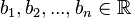 such that
such that
or, equivalently,
where 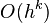 is the error, the difference between the correct answer and the approximation, expressed using Big-O notation. Because
is the error, the difference between the correct answer and the approximation, expressed using Big-O notation. Because 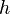 may be presumed to be small, a larger value for
may be presumed to be small, a larger value for 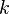 is better than a smaller value.
is better than a smaller value.
A general method for finding the coefficients is to generate the Taylor expansion of 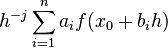 and choose
and choose 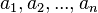 and
and 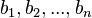 such that
such that 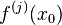 and the remainder term are the only non-zero terms. If there are no such coefficients, a smaller value for
and the remainder term are the only non-zero terms. If there are no such coefficients, a smaller value for 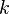 must be chosen.
must be chosen.
For a function of 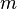 variables
variables 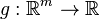 , the procedure is similar, except
, the procedure is similar, except 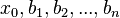 are replaced by points in
are replaced by points in 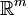 and the multivariate extension of Taylor's theorem is used.
and the multivariate extension of Taylor's theorem is used.
Single-Variable
In all single-variable examples, 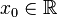 and
and 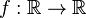 are unknown, and
are unknown, and 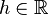 is small. Additionally, let
is small. Additionally, let  be 5 times continuously differentiable on
be 5 times continuously differentiable on 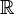 .
.
First Derivative
Find 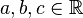 such that
such that 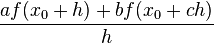 best approximates
best approximates 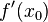 .
.
First, we find the Taylor series expansion of 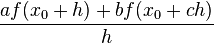 with remainder term to be
with remainder term to be
If we can find a solution to the system
then we can substitute that solution into the Taylor expansion to obtain
The system of equations has exactly one solution: 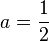 ,
, 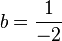 ,
, 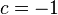 , so
, so
Let 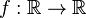 be 42 times continuously differentiable on
be 42 times continuously differentiable on 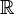 . Find the largest
. Find the largest 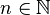 such that
such that
In other words, find the order of the error of the method.
The Taylor expansion of the method is
Simplifying this algebraically gives
The multiple of 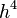 cannot be removed, so
cannot be removed, so 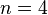 and by properties of Big-O notation,
and by properties of Big-O notation,
Second Derivative
Find 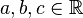 such that
such that 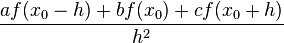 best approximates
best approximates 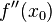 .
.
First, we find the Taylor series expansion of 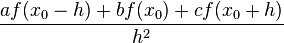 , with remainder term to be
, with remainder term to be
If we can find a solution to the system
then we can substitute that solution into the Taylor expansion and obtain
The system of equations has exactly one solution:  ,
, 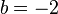 ,
, 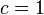 so
so
Multivariate
In all two-variable examples, 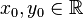 and
and 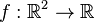 are unknown, and
are unknown, and 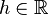 is small.
is small.
Non-Mixed Derivatives
Because of the nature of partial derivatives, some of them may be calculated using single-variable methods. This is done by holding constant all but one variable to form a new function of one variable. For example if 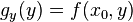 , then
, then 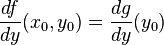 .
.
Find an approximation of 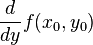
Because we are differentiating with respect to only one variable, we can hold x constant and use the result of one of the single-variable examples:
Mixed Derivatives
Mixed derivatives may require the multivariate extension of Taylor's theorem.
Let 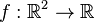 be 42 times continuously differentiable on
be 42 times continuously differentiable on 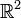 and let
and let 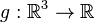 be defined as
be defined as
Find the largest 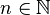 such that
such that
In other words, find the order of the error of the approximation.
The first few terms of the multivariate Taylor expansion of  around
around 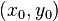 are
are
We substitute the expansion for  into the approximation
into the approximation 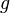 to obtain
to obtain
Because of the careful choices of coefficients, we can simplify this to
We note that Big-O notation permits us to write the last 3 terms as 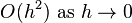 . Thus,
. Thus,
Because the multiples of 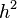 are unaffected by adding more terms to the Taylor expansion,
are unaffected by adding more terms to the Taylor expansion, 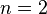 is the greatest natural number satisfying the conditions given in the problem.
is the greatest natural number satisfying the conditions given in the problem.
Example Code
Implementing these methods is reasonably simple in programming languages that support higher-order functions. For example, the method from the first example may be implemented in C++ using function pointers, as follows:
// Returns an approximation of the derivative of f at x.
double derivative (double (*f)(double), double x, double h =0.01) {
return (f(x + h) - f(x - h)) / (2 * h);
}