Error of Analysis of Newton-Cotes formulas
Error Analysis of Newton-Cotes formulas
The Newton-Cotes formulas are a group of formulas for evaluating numeric integration at equally spaced points.
The Methods[1]
Let 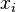 ,
, 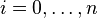 , be
, be 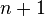 equally spaced points, and
equally spaced points, and 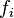 be the corresponding values. Let
be the corresponding values. Let 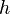 be the space
be the space 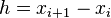 , and let
, and let  be the interpolation variable
be the interpolation variable 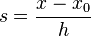 . Thus to interpolate at x,
. Thus to interpolate at x,
A polynomial 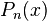 of degree
of degree  can be derived to pass through these points and approximate the function
can be derived to pass through these points and approximate the function  . Using divided differences and Newton polynomial,
. Using divided differences and Newton polynomial, 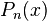 can be obtained as
can be obtained as
From the general form of polynomial interpolation error, the error of using 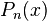 to interpolate
to interpolate  can be obtained as
can be obtained as
where 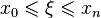 .
.
Since 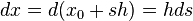 , the error term of numerical integration is
, the error term of numerical integration is
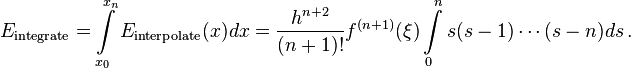
(1 )
Error terms for different rules
The Trapezoid Rule
Let's consider the trapezoid rule in a single interval. In each interval, the integration uses two end points. Thus 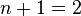 . Then
. Then 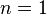 . Applying (1
), we get
. Applying (1
), we get
where 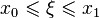 .
Thus the local error is
.
Thus the local error is 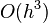 . Consider the composite trapezoid rule. Given that
. Consider the composite trapezoid rule. Given that 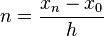 , the global error is
, the global error is
![\begin{align}\left|\sum_{i=0}^{n-1} -\frac{1}{12}h^3f''(\xi_i)\right|&=n[-\frac{1}{12}(x_n-x_0)h^2f''(\bar{\xi})]\\
&=-\frac{1}{12}(x_n-x_0)h^2f''(\bar{\xi})=O(h^2)\,,\end{align}](../I/m/c8db1265d1e8db17a6b7caef0c7f53d6.png)
(2 )
where 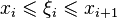 ,
, 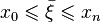 .
.
To justify (2
), we can need the theorem below[2] in page 345:
Ifis continuous and the
, then for some value
in the interval of all the arguments
The Simpson's 1/3 Rule
Consider Simpson's 1/3 rule. In this case, three equally spaced points are used for integration. Thus 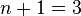 . Applying (1
), we get
. Applying (1
), we get
where 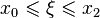 .
.
This doesn't mean that the error is zero. It simply means that the cubic term is identically zero. The error term can be obtained from the next term in the Newton polynomial, obtaining
Thus the local error is 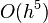 and the global error is
and the global error is 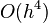 .
.
The Simpson's 3/8 Rule
Consider Simpson's 3/8 rule. In this case, 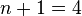 since four equally spaced points are used. Applying (1
), we get
since four equally spaced points are used. Applying (1
), we get
where 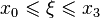 .
.
Both the Simpon's 1/3 rule and the 3/8 rule have error terms of order 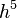 . With smaller coefficient, the 1/3 rule seems more accurate. Then why do we need the 3/8 rule? The 3/8 rule is useful when the total number of increments
. With smaller coefficient, the 1/3 rule seems more accurate. Then why do we need the 3/8 rule? The 3/8 rule is useful when the total number of increments  is odd. Three increments can be used with the 3/8 rule, and then the rest even number of increments can be used with 1/3 rule.
is odd. Three increments can be used with the 3/8 rule, and then the rest even number of increments can be used with 1/3 rule.
A Numerical Example
Given the set of data points, solve the numerical integration 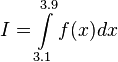
 | 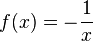 |
|---|---|
| 3.1 | -0.32258065 |
| 3.5 | -0.28571429 |
| 3.9 | -0.25641026 |
Solution
Use the trapezoid rule. First try 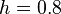 . That is, use only the two end points. We can get
. That is, use only the two end points. We can get
Compared with the exact solution 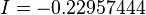 we have
we have
Using all three points with 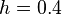 we can get
we can get
and so
Thus the error ratio is 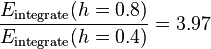 . This is close to what we can get by inspecting
. This is close to what we can get by inspecting
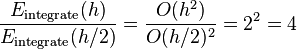 .
.
Exercises
Exercise 1[3]
Using the data given below, find the maximum error incurred in using Newton's forward interpolation formula to approximate 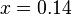 .
.
 |  |
|---|---|
| 0.1 | 1.10517 |
| 0.2 | 1.22140 |
| 0.3 | 1.34986 |
| 0.4 | 1.49182 |
| 0.5 | 1.64872 |
Solution:
According the general error formula of polynomial interpolation
where ![x \in [0.1,0.5]](../I/m/5503b57053eec1fcd5cb4485ca138c43.png) .
.
Given that 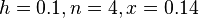 , and
, and 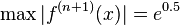 , we can get
, we can get
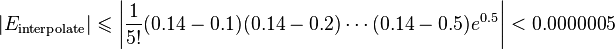 .
.
Exercise 2
When using Simpson's 1/3, what is the error ratio supposed to be?
Solution:
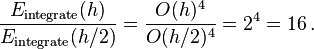
References
- ↑ Hoffman, Joe D. (2001). Numerical Methods for Engineers and Scientists (2nd ed.). Marcel Derkker, INC. ISBN 0-8247-0443-6.
- ↑ Hamming, R. W. (1986). Numerical Methods for Scientists and Engineers (2nd ed.). New York: Dover Publications, INC. ISBN 0-486-65241-6. http://books.google.com/books/about/Numerical_Methods_for_Scientists_and_Eng.html?id=Y3YSCmWBVwoC.
- ↑ Tenenbaum, Morris; Pollard, Harry (1985). Ordinary Differential Equations: An Elementary Textbook for Students of Mathematics, Engineering, and the Sciences. New York: Dover Publications, INC. ISBN 0-786-64940-7.
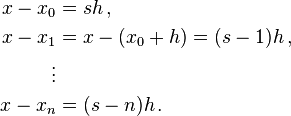
![\begin{align}P_n(x)&=[f_0]+[f_0,f_1](x-x_0)+\cdots+[f_0,\ldots,f_n](x-x_0)(x_1)\ldots(x-x_{n-1})\\
&=[f_0]+[f_0,f_1]sh+\cdots+[f_0,\ldots,f_n]s(s-1)\ldots(s-n+1)h^n\,.\end{align}](../I/m/81995b75c7f6e447b794e5c0fc2b6949.png)
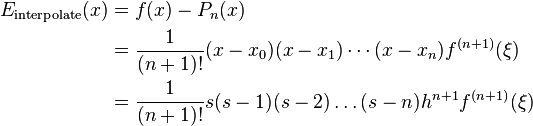
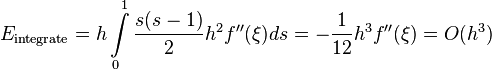
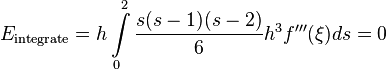
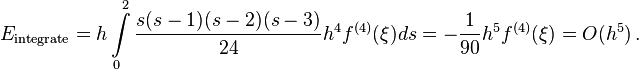
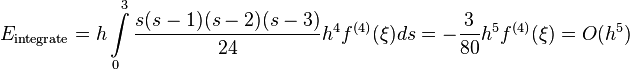
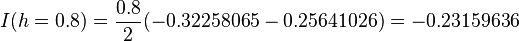
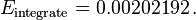
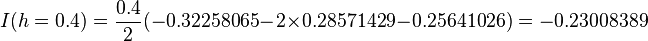
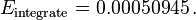
![|E_{\text{interpolate}}| \leqslant \left|\frac{1}{(n+1)!}(x-x_0)(x-x_1)\cdots (x-x_n)\right|[\max| f^{(n+1)}(x)|]](../I/m/f16411988d476a867a55b54347eaaf55.png)