Thermodynamics/The First Law Of Thermodynamics

Introduction

 Thermodynamics = study of the transformation of E. from one form to another, and from one system to another.

 Thermal energy = E. associated with motion of atoms and molecules in a substance.

Thermodynamic systems

• System = definite quantity of mass bounded by a real or imaginary closed surface.

• Surrounding = any systems that can interchange E. with a given system.

• A system exchange E. with surroundings by doing mechanical work or by heat flow.

• If no E. interchange takes place, then the system is isolated.

Thermodynamic coordinates (state variables)

They are the values that determine the state of a system (e.g. P, T , V, mass and density).

Properties

Macroscopic properties

Gross quantities of the system, measured by lab operations. (e.g. P, V, T, m).

Microscopic properties

Quantities that describe the atoms and molecules of the system and their properties (e.g. m and v of molecules).

Processes

Process = change in the thermodynamics coordinates.

Reversible process

Process in which the system is always in equilibrium with its surrounding.

Irreversible process

Process in which the system is not in equilibrium with its surroundings.

Occurs when the change in thermodynamic coordinates is large and sudden.

Equation of state

• It is a relation between P, V and T of a substance.

• It exists for every homogenous substance.

• E.g. P may be considered as a function of V and T: P = f (V,T).

• A perfect gas is one in which intermolecular forces are considered negligible.

       Common forms of the equation of state of an ideal gas: PV = nRuT
                                                              PV = mRT
       where n is the number of moles, Ru is the universal gas constant, and R is the specific gas constant.
       The universal and specific gas constants are related as follows: R=Ru/M, where M is the molecular weight 
       of the gas.
       Using this relation and the fact that n=m/M, the two equations above can be derived from each other.
       The value of the universal gas constant is:
                                                              Ru=8314J/(kg*mole*K)=4.97*10^4(ft*lb)/(slug*mole*R)
       Note: Some textbooks do a poor job of specifying whether to use the universal or specific gas constant.  Remember
       that if the equation contains mass (or density) use the specific gas constant.  If the equation contains the number of
       moles, use the universal gas constant.  If you still aren't certain, make sure the units check out.

• State function = function that depends only on the state of the system and does not vary as long as the system has definite and fixed state variables.

Mechanical work

Consider a gas in a cylindrical piston. F = p A ---> dW = F dx = p A dx = p dV ---> W = ∫ p dV (= area under p–V curve).

Work done by the gas

The gas expands.

Work is +ve.

Work done on the gas

The gas contracts.

Work is –ve.

Work and heat depend on path

• From initial state a to final state c, a system may take path

o a b c, doing greatest work.

o a d c, doing minimal work.

o a c, doing intermediate work.

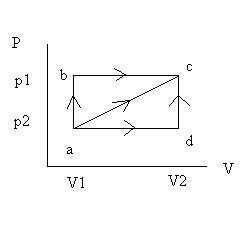
• Work thus depends not only on final and initial states but also on intermediate ones. Work is thus not a property of a system.

• Same result follows by computing flow of heat during the process. Thus, both work and heat depend on path and neither can be conserved alone.

• Notes:

o Work = E. transmitted from one system to another so that a difference in T is not directly involved.

o Values of specific heat depend on conditions:

At constant volume (isometric)

Qv = n cv ∆T

cv = molar specific heat at constant V

At constant pressure (isobaric)

Qp = n cp ∆T

cp = molar specific heat at constant P

Note that

cp = cv + R , Qv + p∆V = Qp, but ∆T = ∆T.

The First Law of Thermodynamics

• For an Isolated System, when heat is transformed into other types of Energy the Total Energy (E_T) remains Constant.
• The Change in the System's Internal Energy (∆U) is independent of the method of change, because it can be obtained through:
  • A Change in Heat (Q).
  • Work done on/by the System, on its Surroundings.
  • or Both

• Initial and final internal Energy depend only on changes in T, P, and V.
• If an amount of heat Q is supplied to a system, it expands and does an amount of work W.

Mathematically:

∆U = U_f – U_i = Q + W_Net

Where:

• U_i: Initial Internal Energy
• U_f: Final Internal Energy
• ∆U: Change in Internal Energy
  • ∆U > 0: Internal Energy is increased.
  • ∆U < 0, Internal Energy is decreased.

• Q: Heat Added.

• W_Net: Net Work by/on the system.
  • W_Net > 0: Work On System. (Energy Entering the System)
  • W_Net < 0: Work By System. (Energy Exiting the System)

Caution: The equation and Work definitions must be compatible. If one uses a negative work equation, one must inverse the the definitions as well.

1^st Law Practice Problems

Q: Which of the following would increase the Internal Energy of a System by 5(J)?

A:

1. Heat the System, 20(J), and have it do 15(J) of work. (True, ΔU = +5J)
2. Heat the System, 20(J), and do 15(J) of work on it. (False, ΔU = +35J)
3. Cool the System, 20(J), and have it do 15(J) of work. (False, ΔU = -35J)
4. Cool the System, 20(J), and do 15(J) of work on it. (False, ΔU = -5J)

Applications of the First Law of Thermodynamics

1) Isometric process:

• It occurs at constant V. Thus, W = 0.

• From the 1st rule of thermodynamics,

∆U = Q_v = n cv ∆T

• Quantity of heat supplied to a system at constant V is thus equal to the increase in the internal E. of the system.

2) Isobaric process:

• It occurs at constant P. e.g. water boiled and vaporized in a steam engine.

• W = ∫ P dV = P ∫ dV = P (V_f – V_i) ; Q = m L_v.

• From the 1st rule of thermodynamics,

∆U = m L_v – p (V_f – Vi)

Where V_f = volume of vapor, V_i = volume of liquid.

3) Cyclic process:

• In which final state and initial state are the same. Since internal E. is a state function, internal E. doesn’t change during cyclic process. Thus, ∆U = 0.

• From the 1st rule of thermodynamics,

Q = W

• Thus, in a cyclic process, the amount of heat gained or lost through the cycle is equal to the amount of work done = area enclosed by the cycle.

4) Isothermal process:

• It occurs at constant T. e.g. in thermostats. Thus dT = 0.

• P = n R T / V ---> WT = ∫ (n R T / V) dV = n R T ln (V_f / V_i).

• Since T is constant, P_i V_i = P_f V_f

• (V_f / V_i) = (p_i / p_f).

WT = n R T ln (V_f / V_i) = n R T ln (p_i / p_f)

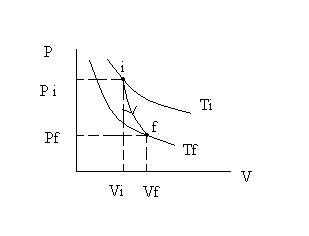
5) Adiabatic process :

• It occurs so that no heat flows into or out of the system. E.g. by sealing the system off from its surroundings with insulating material or by performing the process quickly (because flow of heat is slow). Thus Q = 0.

• From 1st rule of thermodynamics,

∆U = U_f – U_i = – W

• Thus, if work is done on the system, internal E. increases by exactly the amount of work done on the system.

• If work is done by the system (gas expand), internal E. decreases by exactly the amount of external work it does.

Heat content or Enthalpy

• In isobaric process,

Q_p = ∆U – W = (U_f – U_i) + p (V_f – V_i)

Q_p = (U_f + p V_f) – (U_i + p V_i)

But H = U + pV ; where H = enthalpy = state function depending only on the state of the system and not on the path taken. Thus,

Q_p = H_f – H_i = ∆H

• Thus, heat gained or lost in any isobaric process = change in enthalpy of the system.

• In endothermic reaction, heat is gained by system, so Q_p > 0 and enthalpy increases.

• In exothermic reaction, heat is lost by system, so Q_p < 0 and enthalpy decreases.

Molar specific heats of an ideal gas

• Gas can be heated to a temp. T isometrically or isobarically.

• In isometric process, dUv = n cv dT.

• In isobaric process, dUp = n cp dT – p dV.

• From ideal gas equation, p V = n R T  p dV = n R dT.

• Thus, for isobaric process, dUp = n cp dT – n R dT.

• Internal E. depends only on T  change in internal E. is the same in both process.

• Thus, dUv = dUp  n cv dT = n cp dT – n R dT  cp – cv = R.

• For ideal gas, U = (3/2) n R T. Thus,

cv = (1 / n) ( dU / dT) = (1 / n) d / dT[(3 / 2) ( n R T)] = (3 / 2) R And cp = cv + R = (5 / 2) R.

• γ = cp / cv. (constant). cv, cp and γ vary according to type of gas:

Monoatomic gas

cv = (3 / 2) R

cp = (5 / 2) R

γ = 5 / 3 = 1.67

Diatomic gas

cv = (5 / 2) R

cp = (7 / 2) R

γ = 7 / 5 = 1.40

Polyatomic gas

cv = (7 / 2) R

cp = (9 / 2) R

γ = 9 / 7 = 1.29

Adiabatic processes for an ideal gas

Adiabatic ---> Q = 0 ; W = p dV ---> dU = n cv dT = - p dV ---> dT = - p dV / n cv.

Since p V = n R T ---> p dV + V dp = n R dT = – (R / cv) p dV. Since R = cp – cv,

p dV + V dp = - [(cp – cv) / cv] p dV = (1 – γ) p dV. Dividing by (p V),

dV / V + dp / p = (1 – γ) dV / V ---> (dp / p) + (γ dV / V) = 0. Integrating the eqn,

ln p + γ ln V = constant ----> p (V) ^ γ = constant. Thus,

pi (Vi) ^ γ = pf (Vf) ^ γ

But p = n R T / V. Thus,

Ti (Vi) ^ (γ – 1) = Tf (Vf) ^ (γ – 1)

For isothermal process, p V = constant ----> p dV + V dp = 0.

Slopeisothermal = dp / dV ---> Slopeisothermal = – p / V.

For adiabatic process, p V ^ γ = constant ---> γ p (V) ^ (γ – 1) + (V ^ γ) dp = 0

Slopeadiabatic = dp / dV ---> Slopeadiabatic = – γ (p / V). Thus,

Slopeisothermal / Slopeadiabatic = γ

Note:

Wadiabatic = (pi Vi – pf Vf) / γ – 1

External Links

UC Davis Thermal Energy Wiki - http://chemwiki.ucdavis.edu/Physical_Chemistry/Thermodynamics/State_Functions/THERMAL_ENERGY

Energy/Watt Calculator - http://www.mhi-inc.com/Converter/watt_calculator.htm