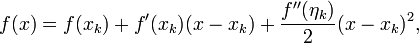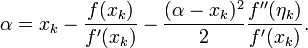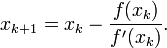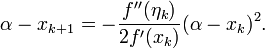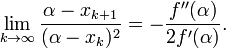The Newton's method
Numerical analysis > The Newton's method
Newton's method generates a sequence 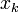 to find the root
to find the root 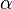 of a function
of a function 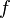 starting from an initial guess
starting from an initial guess 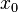 . This initial guess
. This initial guess 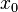 should be close enough to the root
should be close enough to the root 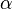 for the convergence to be guaranteed. We construct the tangent of
for the convergence to be guaranteed. We construct the tangent of 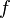 at
at 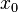 and we find an approximation of
and we find an approximation of 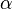 by computing the root of the tangent. Repeating this iterative process we obtain the sequence
by computing the root of the tangent. Repeating this iterative process we obtain the sequence 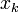 .
.
Derivation of Newton's Method
Approximating 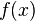 with a second order Taylor expansion around
with a second order Taylor expansion around 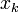 ,
,
with 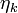 between
between 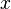 and
and 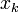 .
Imposing
.
Imposing  and recalling that
and recalling that 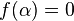 , with a little rearranging we obtain
, with a little rearranging we obtain
Neglecting the last term, we find an approximation of 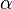 which we shall call
which we shall call 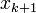 . We now have an iteration which can be used to find successively more precise approximations of
. We now have an iteration which can be used to find successively more precise approximations of 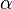 :
:
Newton's method :
Convergence Analysis
It's clear from the derivation that the error of Newton's method is given by
Newton's method error formula:
From this we note that if the method converges, then the order of convergence is 2. On the other hand, the convergence of Newton's method depends on the initial guess 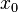 .
.
The following theorem holds
Theorem
Assume that 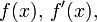 and
and 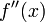 are continuous in neighborhood of the root
are continuous in neighborhood of the root 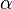 and that
and that 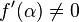 . Then, taken
. Then, taken 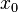 close enough to
close enough to 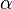 , the sequence
, the sequence 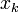 , with
, with 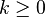 , defined by the Newton's method converges to
, defined by the Newton's method converges to 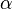 . Moreover the order of convergence is
. Moreover the order of convergence is 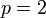 , as
, as
Advantages and Disadvantages of Newton's Method
Advantages of using Newton's method to approximate a root rest primarily in its rate of convergence. When the method converges, it does so quadratically. Also, the method is very simple to apply and has great local convergence.
The disadvantages of using this method are numerous. First of all, it is not guaranteed that Newton's method will converge if we select an 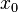 that is too far from the exact root. Likewise, if our tangent line becomes parallel or almost parallel to the x-axis, we are not guaranteed convergence with the use of this method. Also, because we have two functions to evaluate with each iteration (
that is too far from the exact root. Likewise, if our tangent line becomes parallel or almost parallel to the x-axis, we are not guaranteed convergence with the use of this method. Also, because we have two functions to evaluate with each iteration (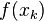 and
and 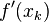 , this method is computationally expensive. Another disadvantage is that we must have a functional representation of the derivative of our function, which is not always possible if we working only from given data.
, this method is computationally expensive. Another disadvantage is that we must have a functional representation of the derivative of our function, which is not always possible if we working only from given data.