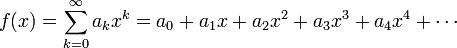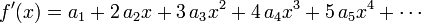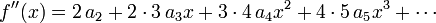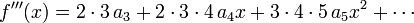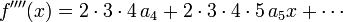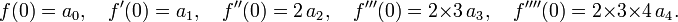Taylor's series
A well-behaved function can be expanded into a power series. This means that for all non-negative integers 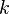 there are real numbers
there are real numbers 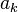 such that
such that
Let us calculate the first four derivatives using 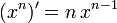 :
:
Setting  equal to zero, we obtain
equal to zero, we obtain
Let us write 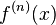 for the
for the  -th derivative of
-th derivative of 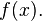 We also write
We also write 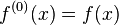 — think of
— think of  as the "zeroth derivative" of
as the "zeroth derivative" of 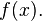 We thus arrive at the general result
We thus arrive at the general result 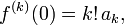 where the factorial
where the factorial 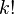 is defined as equal to 1 for
is defined as equal to 1 for  and
and  and as the product of all natural numbers
and as the product of all natural numbers 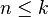 for
for 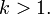 Expressing the coefficients
Expressing the coefficients 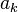 in terms of the derivatives of
in terms of the derivatives of  at
at 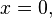 we obtain
we obtain
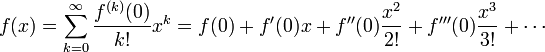 |
This is the Taylor series for 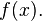
A remarkable result: if you know the value of a well-behaved function  and the values of all of its derivatives at the single point
and the values of all of its derivatives at the single point 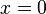 then you know
then you know  at all points
at all points 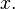 Besides, there is nothing special about
Besides, there is nothing special about 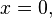 so
so  is also determined by its value and the values of its derivatives at any other point
is also determined by its value and the values of its derivatives at any other point 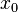 :
:
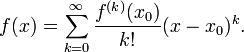 |