Table of physical constants
Table of universal constants
| Quantity | Symbol | Value | Relative Standard Uncertainty |
|---|---|---|---|
| characteristic impedance of vacuum | 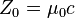 | 376.730 313 461... Ω | defined |
| electric constant (permittivity of free space) | 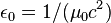 | 8.854 187 817... × 10-12F·m-1 | defined |
| magnetic constant (permeability of free space) | 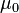 | 4π × 10-7 N·A-2 = 1.2566 370 614... × 10-6 N·A-2 | defined |
| Newtonian constant of gravitation | 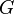 | 6.6742(10) × 10-11m3·kg-1·s-2 | 1.5 × 10-4 |
| Planck's constant | 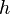 | 6.626 0693(11) × 10-34 J·s | 1.7 × 10-7 |
| Dirac's constant | 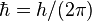 | 1.054 571 68(18) × 10-34 J·s | 1.7 × 10-7 |
| speed of light in vacuum |  | 299 792 458 m·s-1 | defined |
Table of electromagnetic constants
| Quantity | Symbol | Value1 (SI units) | Relative Standard Uncertainty |
|---|---|---|---|
| Bohr magneton | 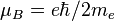 | 927.400 949(80) × 10-26 J·T-1 | 8.6 × 10-8 |
| conductance quantum | 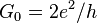 | 7.748 091 733(26) × 10-5 S | 3.3 × 10-9 |
| Coulomb's constant | 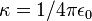 | 8.987 742 438 × 109 N·m2C-2 | defined |
| elementary charge |  | 1.602 176 53(14) × 10-19 C | 8.5 × 10-8 |
| Josephson constant | 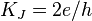 | 483 597.879(41) × 109 Hz· V-1 | 8.5 × 10-8 |
| magnetic flux quantum | 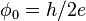 | 2.067 833 72(18) × 10-15 Wb | 8.5 × 10-8 |
| nuclear magneton | 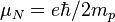 | 5.050 783 43(43) × 10-27 J·T-1 | 8.6 × 10-8 |
| resistance quantum | 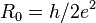 | 12 906.403 725(43) Ω | 3.3 × 10-9 |
| von Klitzing constant | 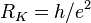 | 25 812.807 449(86) Ω | 3.3 × 10-9 |
Table of atomic and nuclear constants
| Quantity | Symbol | Value1 (SI units) | Relative Standard Uncertainty | |
| Bohr radius | 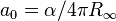 | 0.529 177 2108(18) × 10-10 m | 3.3 × 10-9 | |
| Fermi coupling constant | 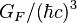 | 1.166 39(1) × 10-5 GeV-2 | 8.6 × 10-6 | |
| fine-structure constant | 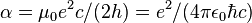 | 7.297 352 568(24) × 10-3 | 3.3 × 10-9 | |
| Hartree energy | 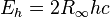 | 4.359 744 17(75) × 10-18 J | 1.7 × 10-7 | |
| quantum of circulation | 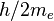 | 3.636 947 550(24) × 10-4 m2 s-1 | 6.7 × 10-9 | |
| Rydberg constant | 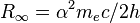 | 10 973 731.568 525(73) m-1 | 6.6 × 10-12 | |
| Thomson cross section | 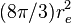 | 0.665 245 873(13) × 10-28 m2 | 2.0 × 10-8 | |
| Weinberg angle|weak mixing angle | 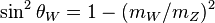 | 0.222 15(76) | 3.4 × 10-3 | |
Table of physico-chemical constants
| Quantity | Symbol | Value1 (SI units) | Relative Standard Uncertainty | |
| atomic mass constant (unified atomic mass unit) | 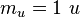 | 1.660 538 86(28) × 10-27 kg | 1.7 × 10-7 | |
| Avogadro's number | 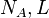 | 6.022 1415(10) × 1023 | 1.7 × 10-7 | |
| Boltzmann constant | 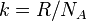 | 1.380 6505(24) × 10-23 J·K-1 | 1.8 × 10-6 | |
| Faraday constant | 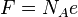 | 96 485.3383(83)C·mol-1 | 8.6 × 10-8 | |
| first radiation constant | 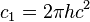 | 3.741 771 38(64) × 10-16 W·m2 | 1.7 × 10-7 | |
| for spectral radiance | 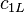 | 1.191 042 82(20) × 10-16 W · m2 sr-1 | 1.7 × 10-7 | |
| Loschmidt constant | at 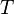 =273.15 K and =273.15 K and 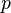 =101.325 kPa =101.325 kPa | 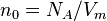 | 2.686 7773(47) × 1025 m-3 | 1.8 × 10-6 |
| gas constant | 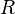 | 8.314 472(15) J·K-1·mol-1 | 1.7 × 10-6 | |
| molar Planck constant | 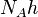 | 3.990 312 716(27) × 10-10 J · s · mol-1 | 6.7 × 10-9 | |
| molar volume of an ideal gas | at 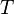 =273.15 K and =273.15 K and 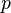 =100 kPa =100 kPa | 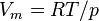 | 22.710 981(40) × 10-3 m3 ·mol-1 | 1.7 × 10-6 |
at 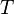 =273.15 K and =273.15 K and 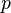 =101.325 kPa =101.325 kPa | 22.413 996(39) × 10-3 m3 ·mol-1 | 1.7 × 10-6 | ||
| Sackur-Tetrode constant | at 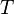 =1 K and =1 K and 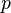 =100 kPa =100 kPa | 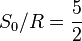 ![+ \ln\left[ (2\pi m_u k T / h^2)^{3/2} k T / p \right]](../I/m/358b3e034bd9f1c891bbb05233461a70.png) | -1.151 7047(44) | 3.8 × 10-6 |
at 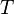 =1 K and =1 K and 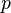 =101.325 kPa =101.325 kPa | -1.164 8677(44) | 3.8 × 10-6 | ||
| second radiation constant | 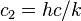 | 1.438 7752(25) × 10-2 m·K | 1.7 × 10-6 | |
| Stefan-Boltzmann constant | 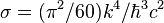 | 5.670 400(40) × 10-8 W·m-2·K-4 | 7.0 × 10-6 | |
| Wien displacement law constant | 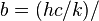 4.965 114 231... 4.965 114 231... | 2.897 7685(51) × 10-3 m · K | 1.7 × 10-6 | |
Table of adopted values
| Quantity | Symbol | Value (SI units) | Relative Standard Uncertainty | |
| conventional value of Josephson constant2 | 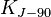 | 483 597.9 × 109 Hz · V-1 | defined | |
| conventional value of von Klitzing constant3 | 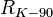 | 25 812.807 Ω | defined | |
| molar mass | constant | 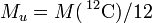 | 1 × 10-3 kg · mol-1 | defined |
| of carbon-12 | 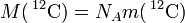 | 12 × 10-3 kg · mol−1 | defined | |
| standard acceleration of gravity (free fall on Earth) | 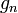 | 9.806 65 m·s-2 | defined | |
| standard atmosphere | 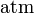 | 101 325 Pa | defined | |
Notes
1The values are given in the so-called concise form; the number in brackets is the standard uncertainty, which is the value multiplied by the relative standard uncertainty.
2This is the value adopted internationally for realizing representations of the volt using the Josephson effect.
3This is the value adopted internationally for realizing representations of the ohm using the quantum Hall effect.
See also
- Coupling constant
- Stellar constants
- Strong gravitational constant
- Vacuum constants
- Physics/Essays/Fedosin/Fine structure constant
- Physics/Essays/Fedosin/Gravitational characteristic impedance of free space
- Physics/Essays/Fedosin/Magnetic coupling constant
- Physics/Essays/Fedosin/Selfconsistent electromagnetic constants
- Physics/Essays/Fedosin/Selfconsistent gravitational constants
- Physics/Essays/Fedosin/Velocity circulation quantum
This article is issued from Wikiversity - version of the Thursday, April 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.