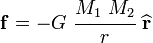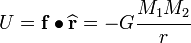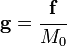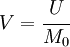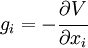Stress function
Stress functions are scalar or vector potential functions that satisfy the equilibrium and compatibility conditions. The stresses can be derived from these functions by taking partial derivatives of the potentials with respect to the spatial coordinates.
Potential functions
You have probably encountered potential functions in introductory physics. Forces can often be calculated assuming the existence of a scalar potential field. One takes the derivative of the potential function with respect to spatial coordinates to get a vector field.
An example is the gravitational potential field.
Consider the gravitational force (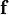
) between two masses (
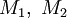) separated by a distance 
.
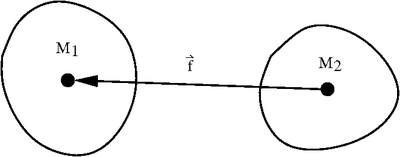 Gravitational force between two masses |
The gravitational potential energy (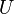
) is a scalar given by
The gravitational field (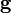
) (due to the effect of many masses), at a point (per unit mass 
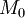) is
The gravitational potential (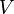
) is a scalar function of position
The work done by the gravitational force equals the decrease in gravitational potential energy.
The scalar gravitational potential can be used to find the vector gravitational field.
Stress functions
Stress functions are very similar to other scalar potential functions such as the gravitational potential. However, instead of delivering a vector field upon differentiation, stress functions deliver a second-order tensor field.
Here are some facts about most stress functions:
- Scalar potential functions that can be used to determine the stress field.
- No obvious physical meaning other than their use in defining stress components in terms of derivatives.
- The only restriction on the choice of a stress function is that the stress components must be defined in terms of the second derivatives of a scalar.
- This is because the second derivatives of a scalar form the components of a second-order tensor.
- Why is such a restriction necessary? To preserve the rules for coordinate transformations.