Strength of materials/Lesson 3a

Here we will look at axially loaded members, or members that only carry tensile or compressive loads.

Basic Equations

There are a few basic equations that every student of material mechanics must know. They are the following:

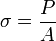$\sigma = \frac{P}{A}~$ (normal stress)
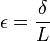$\epsilon = \frac{\delta}{L}~$ (axial strain)
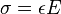$\sigma = \epsilon E~$ (Hooke's Law)

Other equations can be derived from these basic equations:

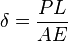$\delta = \frac{PL}{AE}$ (elongation of member)
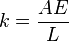$k=\frac{AE}{L}$ (stiffness of member)
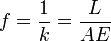$f=\frac{1}{k}=\frac{L}{AE}$ (flexibility of member)

Cables, which are helically wound strands around a central strand, require the use of an effective area and an effective modulus of elasticity.

Nonuniform Bars

If a member has several prismatic parts with different axial forces or stiffnesses:

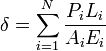
$\delta = \sum_{i=1}^N \frac{P_i L_i}{A_i E_i}$

Or for a continually variable function of length:

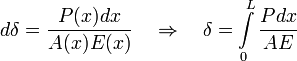
$d\delta = \frac{P(x) dx}{A(x) E(x)} \quad \Rightarrow \quad \delta = \int\limits_0^L \frac{P dx}{AE}$

To illustrate how to solve such problems, let's look at the following example:

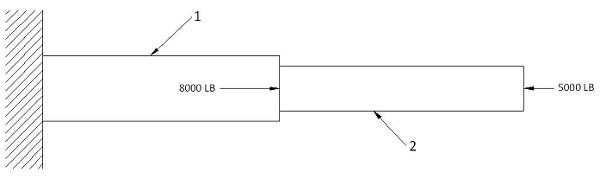
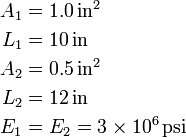
$\begin{align} A_1 & =1.0 \, \text{in}^2\\ L_1 & =10 \, \text{in} \\ A_2 & =0.5 \, \text{in}^2 \\ L_2 & =12 \, \text{in}\\ E_1 & = E_2 = 3\times10^6 \, \text{psi} \end{align}$

We apply the following equations:

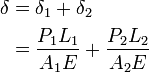
$\begin{align} \delta & = \delta_1 + \delta_2 \\ & = \frac{P_1 L_1}{A_1 E} + \frac{P_2 L_2}{A_2 E} \end{align}$

In order to analyze all the forces, we have to make 2 free body diagrams:

Looking in the x-direction, we can solve for P₁:

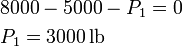
$\begin{align} & 8000-5000-P_1=0\\ & P_1 = 3000 \, \text{lb} \end{align}$

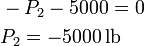
$\begin{align} & -P_2 - 5000 = 0 \\ & P_2 = - 5000 \, \text{lb} \end{align}$

Substituting back into our first equation:

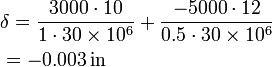
$\begin{align} & \delta = \frac{3000 \cdot 10}{1 \cdot 30 \times 10^6} + \frac{-5000 \cdot 12}{0.5 \cdot 30 \times 10^6} \\ & = -0.003 \, \text{in} \end{align}$

The negative elongation indicates that the total member length is shortened due to the loading.

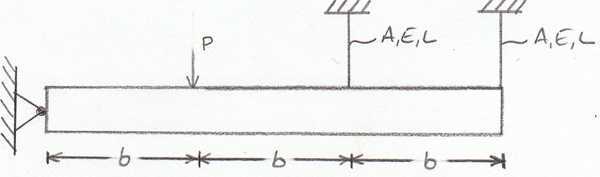
Statically Indeterminate Structures

Some structures cannot be simply determined by the equations of static equilibrium alone. Usually in these cases the number of unknowns are greater than the number of unique equations we can build from static equilibrium. This is called a statically indeterminate structure. In most cases, we can use the equations of axial loading to be able to obtain enough equations to solve for all the unknowns. Let's consider the following example:

This article is issued from Wikiversity - version of the Saturday, January 22, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.