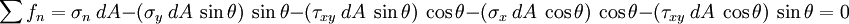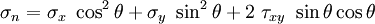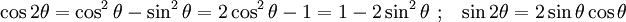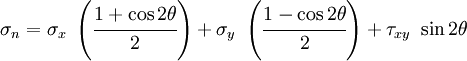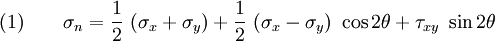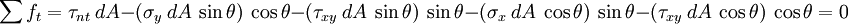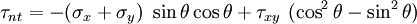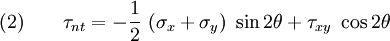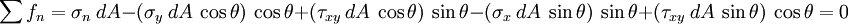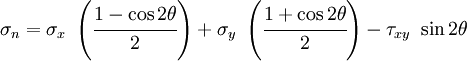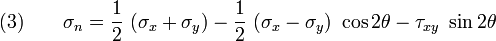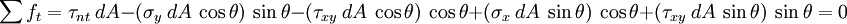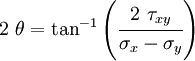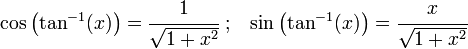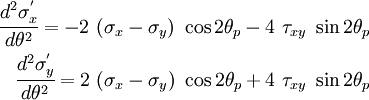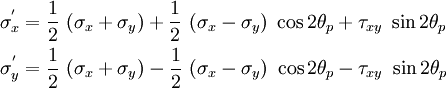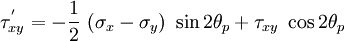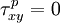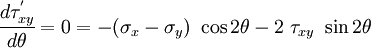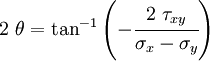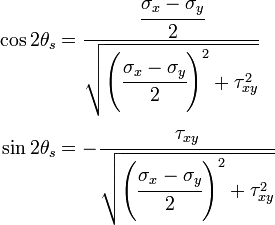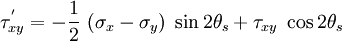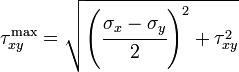Strength of materials/Lesson 3

Lesson 3: Stress transformation and Mohr's circle

Last time we talked about Hooke's law and plane stress. We also discussed how the normal and shear components of stress change depending on the orientation of the plane that they act on. In this lecture we will talk about stress transformations for plane stress.

For the rest of this lesson we assume that we are dealing only with plane stress, i.e., there are only three nonzero stress components 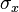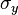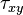$\sigma_x$ , $\sigma_y$ , $\tau_{xy}$ . We also assume that these three components are known.

We want to find the planes on which the stresses are most severe and the magnitudes of these stresses.

Stress transformation rules

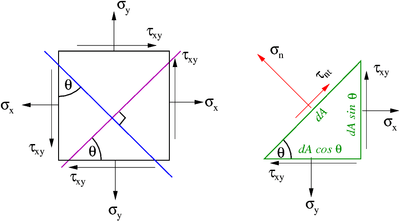
Let us consider an arbitrary plane inside an infinitesimal element. Let this plane be inclined at an angle 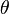$\theta$ to the vertical face of the element. A free body diagram of the region to the left of this plane is shown in the figure below.

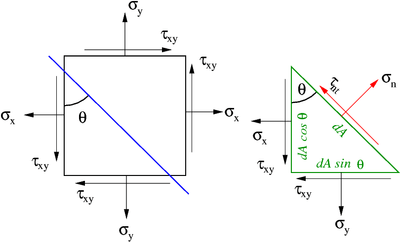Stress transformation

A balance of forces on the free body in the $n$ -direction gives us

\sum f_n = \sigma_n~dA - (\sigma_y~dA~\sin\theta)~\sin\theta - (\tau_{xy}~dA~\sin\theta)~\cos\theta - (\sigma_x~dA~\cos\theta)~\cos\theta - (\tau_{xy}~dA~\cos\theta)~\sin\theta = 0

or,

\sigma_n = \sigma_x~\cos^2\theta + \sigma_y~\sin^2\theta + 2~\tau_{xy}~\sin\theta\cos\theta

Using the trigonometric identities

\cos 2\theta = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta ~;~~ \sin 2\theta = 2\sin\theta\cos\theta

we get

\sigma_n = \sigma_x~\left(\cfrac{1 + \cos 2\theta}{2}\right) + \sigma_y~\left(\cfrac{1 - \cos 2\theta}{2}\right) + \tau_{xy}~\sin 2\theta

or,

\text{(1)} \qquad \sigma_n = \frac{1}{2}~(\sigma_x + \sigma_y) + \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta + \tau_{xy}~\sin 2\theta

Similarly, a balance of forces in the 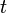$t$ -direction leads to

\sum f_t = \tau_{nt}~dA - (\sigma_y~dA~\sin\theta)~\cos\theta - (\tau_{xy}~dA~\sin\theta)~\sin\theta - (\sigma_x~dA~\cos\theta)~\sin\theta - (\tau_{xy}~dA~\cos\theta)~\cos\theta = 0

\tau_{nt} = -(\sigma_x + \sigma_y)~\sin\theta\cos\theta + \tau_{xy}~(\cos^2\theta - \sin^2\theta)

or,

\text{(2)} \qquad \tau_{nt} = -\frac{1}{2}~(\sigma_x + \sigma_y)~\sin 2\theta + \tau_{xy}~\cos 2\theta

Now let us look at a section that is perpendicular to the one we have looked at. This situation is shown in the figure below.

Stress transformation

In this case, a balance of forces on the free body in the $n$ -direction gives us

\sum f_n = \sigma_n~dA - (\sigma_y~dA~\cos\theta)~\cos\theta + (\tau_{xy}~dA~\cos\theta)~\sin\theta - (\sigma_x~dA~\sin\theta)~\sin\theta + (\tau_{xy}~dA~\sin\theta)~\cos\theta = 0

or,

\sigma_n = \sigma_x~\sin^2\theta + \sigma_y~\cos^2\theta - 2~\tau_{xy}~\sin\theta\cos\theta

or,

\sigma_n = \sigma_x~\left(\cfrac{1 - \cos 2\theta}{2}\right) + \sigma_y~\left(\cfrac{1 + \cos 2\theta}{2}\right) - \tau_{xy}~\sin 2\theta

or,

\text{(3)} \qquad \sigma_n = \frac{1}{2}~(\sigma_x + \sigma_y) - \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta - \tau_{xy}~\sin 2\theta

A balance of forces in the $t$ -direction gives

\sum f_t = \tau_{nt}~dA - (\sigma_y~dA~\cos\theta)~\sin\theta - (\tau_{xy}~dA~\cos\theta)~\cos\theta + (\sigma_x~dA~\sin\theta)~\cos\theta + (\tau_{xy}~dA~\sin\theta)~\sin\theta = 0

or,

\tau_{nt} = -(\sigma_x - \sigma_y)~\sin\theta\cos\theta + \tau_xy~(\cos^2\theta - \sin^2\theta)

or,

\text{(4)} \qquad \tau_{nt} = -\frac{1}{2}~(\sigma_x + \sigma_y)~\sin 2\theta + \tau_{xy}~\cos 2\theta

From equations (2) and (4) we see that the shear stresses are equal. However the normal stresses on the two planes are different as you can see from equations (1) and (3).

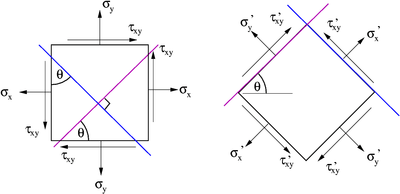
You can think of the two cuts as just the faces of a new infinitesimal element which is at an angle $\theta$ to the original element as can be seen form the following figure.

Stress transformation

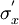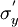If we label the new normal stresses as $\sigma_x^{'}$ and $\sigma_y^{'}$ and the shear stresses as 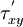$\tau_{xy}^{'}$ , then we can write

\begin{align} \sigma_x^{'} & = \frac{1}{2}~(\sigma_x + \sigma_y) + \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta + \tau_{xy}~\sin 2\theta \\ \sigma_y^{'} & = \frac{1}{2}~(\sigma_x + \sigma_y) - \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta - \tau_{xy}~\sin 2\theta \\ \tau_{xy}^{'} & = -\frac{1}{2}~(\sigma_x - \sigma_y)~\sin 2\theta + \tau_{xy}~\cos 2\theta \end{align}

Maximum normal stresses

What is the orientation of the infinitesimal element that produces the largest normal stress and the largest shear stress? This information can be useful in predicting where failure will occur.

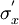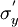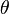To find angle at which we get the maximum/minimum normal stress we can take the derivatives of $\sigma_x^{'}$ and $\sigma_y^{'}$ with respect to $\theta$ and set them to zero. So we have

\begin{align} \cfrac{d\sigma_x^{'}}{d\theta} = 0 = -(\sigma_x - \sigma_y)~\sin 2\theta + 2~\tau_{xy}~\cos 2\theta \\ \cfrac{d\sigma_y^{'}}{d\theta} = 0 = (\sigma_x - \sigma_y)~\sin 2\theta - 2~\tau_{xy}~\cos 2\theta \end{align}

or,

2~\theta = \tan^{-1} \left(\cfrac{2~\tau_{xy}}{\sigma_x - \sigma_y}\right)

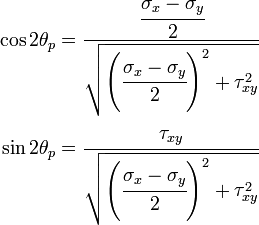
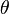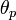The angle at which $\theta$ is a maximum or a minimum is called a principal angle or $\theta_p$ .

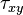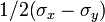Now, from the identities (or we can think in terms of a right angled triangle with a rise of $\tau_{xy}$ and a run of $1/2(\sigma_x - \sigma_y)$ )

\cos\left(\tan^{-1}(x)\right) = \cfrac{1}{\sqrt{1+x^2}} ~;~~ \sin\left(\tan^{-1}(x)\right) = \cfrac{x}{\sqrt{1+x^2}}

we have

\begin{align} \cos 2\theta_p & = \cfrac{\cfrac{\sigma_x - \sigma_y}{2}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \\ \sin 2\theta_p & = \cfrac{\tau_{xy}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \end{align}

Taking another derivative with respect to 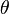$\theta$ we have

\begin{align} \cfrac{d^2\sigma_x^{'}}{d\theta^2} = -2~(\sigma_x - \sigma_y)~\cos 2\theta_p - 4~\tau_{xy}~\sin 2\theta_p \\ \cfrac{d^2\sigma_y^{'}}{d\theta^2} = 2~(\sigma_x - \sigma_y)~\cos 2\theta_p + 4~\tau_{xy}~\sin 2\theta_p \end{align}

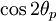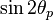Plugging in the expressions for $\cos 2\theta_p$ and $\sin 2\theta_p$ we get

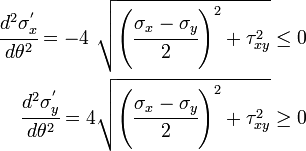
\begin{align} \cfrac{d^2\sigma_x^{'}}{d\theta^2} = -4~ \sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \le 0 \\ \cfrac{d^2\sigma_y^{'}}{d\theta^2} = 4 \sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \ge 0 \end{align}

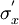Clearly $\sigma_x^{'}$ is a maximum while 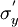$\sigma_y^{'}$ is a minimum value.

Principal stresses

The normal stresses corresponding to the principal angle 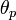$\theta_p$ are called the principal stresses.

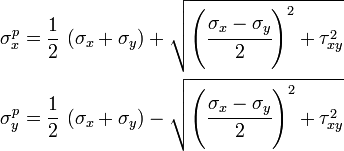
We have

\begin{align} \sigma_x^{'} & = \frac{1}{2}~(\sigma_x + \sigma_y) + \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta_p + \tau_{xy}~\sin 2\theta_p \\ \sigma_y^{'} & = \frac{1}{2}~(\sigma_x + \sigma_y) - \frac{1}{2}~(\sigma_x - \sigma_y)~\cos 2\theta_p - \tau_{xy}~\sin 2\theta_p \end{align}

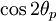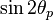Plugging in the expressions for $\cos 2\theta_p$ and $\sin 2\theta_p$ we get

\begin{align} \sigma_x^p & = \frac{1}{2}~(\sigma_x + \sigma_y) + \sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \\ \sigma_y^p & = \frac{1}{2}~(\sigma_x + \sigma_y) - \sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2} \end{align}

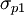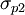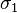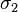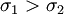These principal stresses are often written as $\sigma_{p1}$ and $\sigma_{p2}$ or $\sigma_1$ and $\sigma_2$ where $\sigma_1 > \sigma_2$ .

The value of the shear stress 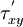$\tau_{xy}^{'}$ for an angle of 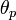$\theta_p$ is

\tau_{xy}^{'} = -\frac{1}{2}~(\sigma_x - \sigma_y)~\sin 2\theta_p + \tau_{xy}~\cos 2\theta_p

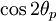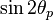Plugging in the expressions for $\cos 2\theta_p$ and $\sin 2\theta_p$ we get

\tau_{xy}^p = 0

Hence there are no shear stresses in the orientations where the stresses are maximum or minimum.

Maximum shear stresses

Similarly, we can find the value of 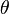$\theta$ which makes the shear stress a maximum or minimum. Thus

\cfrac{d\tau_{xy}^{'}}{d\theta} = 0 = -(\sigma_x - \sigma_y)~\cos 2\theta - 2~\tau_{xy}~\sin 2\theta

2~\theta = \tan^{-1} \left(- \cfrac{2~\tau_{xy}}{\sigma_x - \sigma_y}\right)

In that case

\begin{align} \cos 2\theta_s & = \cfrac{\cfrac{\sigma_x - \sigma_y}{2}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \\ \sin 2\theta_s & = -\cfrac{\tau_{xy}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \end{align}

The value of the shear stress 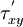$\tau_{xy}^{'}$ for an angle of 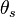$\theta_s$ is

\tau_{xy}^{'} = -\frac{1}{2}~(\sigma_x - \sigma_y)~\sin 2\theta_s + \tau_{xy}~\cos 2\theta_s

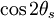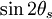Plugging in the expressions for $\cos 2\theta_s$ and $\sin 2\theta_s$ we get

\tau_{xy}^{\text{max}} = \sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}

We can show that this is the maximum value of 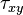$\tau_{xy}$ .

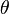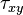Note that, at the value of $\theta$ where $\tau_{xy}$ is maximum, the normal stresses are not zero.

Mohr's circle

Mohr's idea was to express these algebraic relations in geometric form so that a physical interpretation of the idea became easier. The idea was based on the recognition that for an orientation equal to the principal angle, the stresses could be represented as the sides of a right-angled triangle.

Recall that

\begin{align} \cos 2\theta_p & = \cfrac{\cfrac{\sigma_x - \sigma_y}{2}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \\ \sin 2\theta_p & = \cfrac{\tau_{xy}} {\sqrt{\left(\cfrac{\sigma_x - \sigma_y}{2}\right)^2 + \tau_{xy}^2}} \end{align}

We can represent this in graphical form as shown in the figure below. In general, the locus of all points representing stresses at various orientations lie on a circle which is called Mohr's circle.

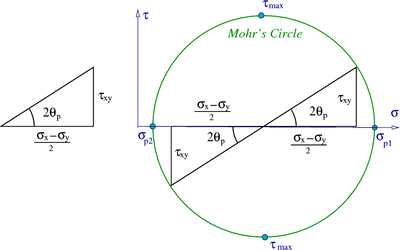Mohr's circle

Notice that we can directly find the largest normal stress and the small normal stress as well as the maximum shear stress directly from the circle. In three-dimensions there are two more Mohr's circles.

Negative shear stress

Also note that there is a region where the shear stress 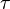$\tau$ is negative. The convention that we follow is that if the shear stress rotates the element clockwise then it is a positive shear stress. If the element is rotated counter-clockwise then the shear stress is negative.

In the next lecture we will get into some more detail about actually plotting Mohr's circles.

External links

Professor Brannon's notes on Mohr's circle

This article is issued from Wikiversity - version of the Thursday, August 30, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.