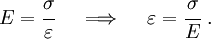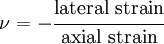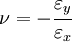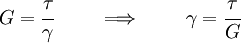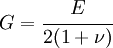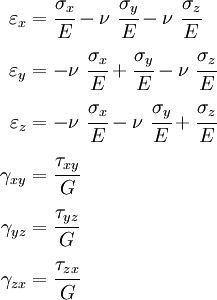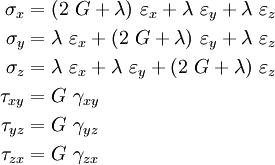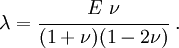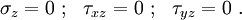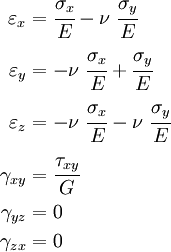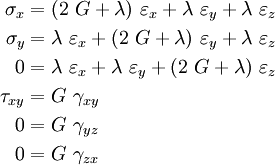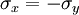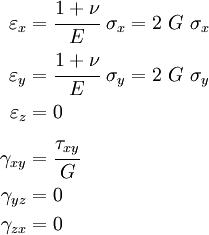Strength of materials/Lesson 2
< Strength of materialsLesson 2: Elastic properties and plane stress
From the previous lesson you know that stress
- is a point quantity.
- has six components - three normal (
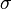 ) and three shear (
) and three shear (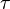 ).
). - components depend on direction.
- acts on a plane.
- has units of force/area.
In this lesson we will introduce you to elastic properties and plane stress.
Elastic Properties
We will deal only with homogeneous and isotropic materials in this course. An isotropic material is one whose properties are independent of direction. Thus, if we want to do a test on a specimen of such a material, it does not matter from which part of the original material or in which direction we cut our sample out.
For an isotropic material we have to deal with three material properties of which only two are independent.
These material properties are
- The Young's modulus (
 ) (also called the modulus of elasticity).
) (also called the modulus of elasticity). - The Poisson's ratio (
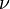 ).
). - The shear modulus (
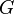 ) (also called the modulus of rigidity).
) (also called the modulus of rigidity).
Young's modulus ( )
)
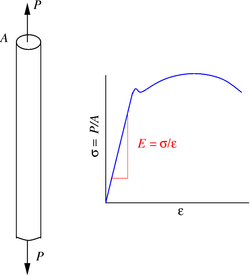 Tension test |
To find the Young's modulus we take a cylindrical specimen and pull on it uniaxially. The result is a stress-strain plot of the form shown in the adjacent figure.
The Young's modulus is defined as the ration of stress to strain in the linear elastic part of the stress-strain curve. Thus
Since the strain is dimensionless, the units of the Young's modulus are the same as the units of stress, i.e., force/area. In the English system, the units of the Young's modulus are psi while the SI units are Pa.
Representative values of Young's modulus are 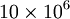 psi (10 Msi) or
psi (10 Msi) or 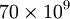 Pa (70 GPa) for
aluminum and
Pa (70 GPa) for
aluminum and 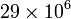 psi (29 Msi) or
psi (29 Msi) or 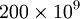 Pa (200 GPa) for steel. The higher the value of
Pa (200 GPa) for steel. The higher the value of  the stiffer a material. Note that stiffness and strength are two different
concepts. Also, the value of Young's modulus does not vary much if the alloying
content of a material is small compared to the amount of pure metal.
the stiffer a material. Note that stiffness and strength are two different
concepts. Also, the value of Young's modulus does not vary much if the alloying
content of a material is small compared to the amount of pure metal.
Poisson's ratio (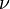 )
)
The Poisson's ratio is defined as
for an applied axial stress.
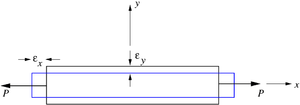 Poisson's ratio. |
For the situation shown in the adjacent figure
Values of Poisson's ratio range between 0.25 to 0.35 for most materials. Also, note that the shape of the cross section does not matter when we are measuring the Poisson's ratio as long as the applied stress is axial.
Shear modulus (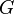 )
)
 Torsion test. |
To find the shear modulus directly, we have to do a torsion test on a cylindrical specimen. A schematic of the stress-strain curve for such a test is shown in the adjacent figure.
The shear modulus is defined as
where  is the shear stress and
is the shear stress and  is the shear strain.
is the shear strain.
The shear modulus can be expressed in terms of  and
and 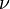 using the relation
using the relation
Hooke's law in three dimensions
The following table shows the strains that result when a stress is applied in a particular direction (or on a particular plane).
| Resulting strain | ||||||
|---|---|---|---|---|---|---|
| Applied stress | 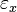 |
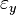 |
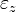 |
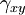 |
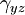 |
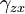 |
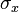 |
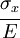 |
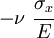 |
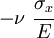 |
0 | 0 | 0 |
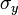 |
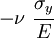 |
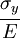 |
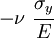 |
0 | 0 | 0 |
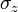 |
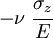 |
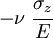 |
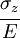 |
0 | 0 | 0 |
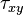 |
0 | 0 | 0 | 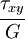 |
0 | 0 |
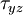 |
0 | 0 | 0 | 0 | 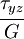 |
0 |
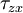 |
0 | 0 | 0 | 0 | 0 | 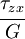 |
You can check that these are indeed correct by looking at an infinitesimal element and seeing what the possible strains are when a particular stress component is applied.
Notice that normal stresses do not produce shear strains and shear stresses do not produce axial strains. This is only true for isotropic materials.
Principle of superposition
One of the advantages of working with linear elastic materials is that we can
apply the principle of superposition. This principle states that the strains
produced by a particular stress state 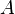 can be added to those produced by a
different stress state
can be added to those produced by a
different stress state 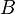 to get the strains for a combined stress state
to get the strains for a combined stress state
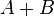 .
.
Applying the principle of superposition to the results in the table above, we find that if we have a stress state where all the stress components are active, then the strains are given by
This relation is called the three-dimensional Hooke's law.
The inverse relation is
where
Plane stress
It helps to think of plane stress as the state of stress on a plane with no stress!
Consider the infinitesimal cube shown in the adjacent figure. Assume that
there is no stress on the plane perpendicular to the 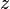 -axis. Then moment
equilibrium requires that the out of plane shear stresses are also zero.
In fact we can simplify the diagram and just draw a square instead of a cube
as shown. But keep in mind that the shear stresses still act on a surface
as do the normal stresses.
-axis. Then moment
equilibrium requires that the out of plane shear stresses are also zero.
In fact we can simplify the diagram and just draw a square instead of a cube
as shown. But keep in mind that the shear stresses still act on a surface
as do the normal stresses.
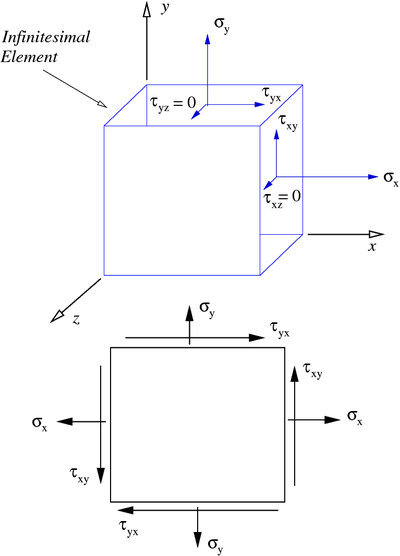 Plane stress. |
Therefore, in a state of plane stress, we have
For plane stress, Hooke's law takes the form
Alternatively,
Effect of zero out of plane strain
Suppose, in addition, that 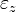 is also zero. What is the effect on
Hooke's law?
is also zero. What is the effect on
Hooke's law?
We then have
Therefore Hooke's law takes the form
We will examine the significance of these relations in the next lesson.