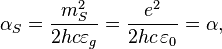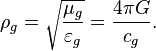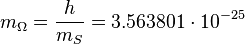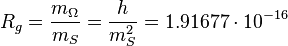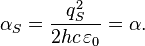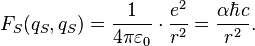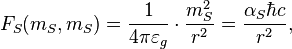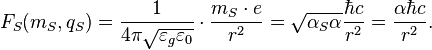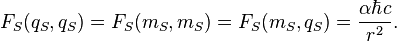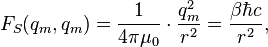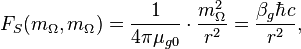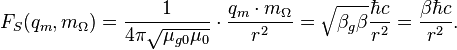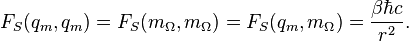Physics/Essays/Fedosin/Stoney scale

< Physics < Essays < Fedosin

In physics, Stoney scale is the fundamental scale, named after the Irish physicist George Johnstone Stoney, who first proposed the ‘’elementary electric charge’’ in 1881. ^[1] It defines that fine structure constant 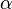$~\alpha$ is equal to gravitational coupling constant (and to electric coupling constant) 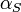$~\alpha_S$ of Stoney scale:

~\alpha_{S} = \frac{m_S^2}{2hc\varepsilon_g}= \frac{e^2}{2hc\,\varepsilon_0} =\alpha,

where

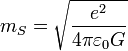$~ m_S = \sqrt{\frac{e^2}{4\pi \varepsilon_0 G}}$ is the Stoney mass;
$~e$ is the elementary charge;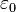
$~\varepsilon_0$ is the vacuum permittivity;
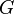$~G$ is the gravitational constant;
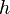$~h$ is the Planck constant;
$~c$ is the speed of light in vacuum;
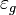$~\varepsilon_g$ is the gravitoelectric gravitational constant.

There is the dimensionless magnetic coupling constant 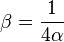$~ \beta =\frac{1} {4\alpha}$ that could be named as the Stoney scale force constant since it defines the force interactions (electric, gravitational, etc.) in the Stoney scale.

History

Contemporary physics has settled on the Planck scale as the most suitable scale for the unified field theory. The Planck scale was however anticipated by George Stoney. ^[1] James G. O’Hara ^[2] pointed out in 1974 that Stoney’s derived estimate of the unit of charge, 10^-20 Ampere (later called the Coulomb), was ¹⁄₁₆ of the correct value of the charge of the electron. Stoney used the quantity 10¹⁸ for the number of molecules presented in one cubic millimeter of gas at standard temperature and pressure. Using Avogadro constant 6.0221×1023
, and the volume of a mole (at standard conditions) of 22.711×106
mm³, we derive, instead of 10¹⁸, the estimate 2.652×1016
. So, if Stoney could use the true number of molecules his estimate of the unit of charge was about ¹⁄₂ of the correct value of the charge.

For a long time the Stoney scale was in the shadow of the Planck scale (something like a "deviation" of it). However, after intensive investigation of gravitation by using the Maxwell-like gravitational equations during last decades, became clear that Stoney scale is independent scale of matter.

Fundamental units of vacuum

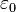The set of primary vacuum constants is: the speed of light $~c$ ; the vacuum permittivity $~\varepsilon_0$ ; the speed of gravity 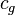$~c_g$ (usually equated to the speed of light); the gravitational constant $~G$ .

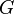The set of secondary vacuum constants is: The vacuum permeability: 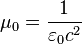$\mu_0 = \frac{1}{\varepsilon_0 c^2}\$ ;

The electromagnetic impedance of free space:

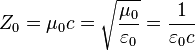Z_0 = \mu_0 c = \sqrt{\frac{\mu_0}{\varepsilon_0}}= \frac{1}{\varepsilon_0 c}

;

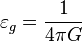The gravitoelectric gravitational constant: $~\varepsilon_g = \frac{1}{4\pi G }$ ;

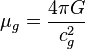The gravitomagnetic gravitational constant: $~\mu_g = \frac{4\pi G }{ c^2_g}$ ;

The gravitational characteristic impedance of free space:

~\rho_g =\sqrt{\frac{\mu_g}{\varepsilon_g}} = \frac{4\pi G }{c_g}.

Note that all Stoney and Planck units are derivatives from the vacuum constants, therefore the last are more fundamental that units of any scale.

If 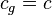$c_g =c$ the above fundamental constants define naturally the following relationship between mass and elementary charge for the Stoney mass:

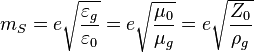m_S = e \sqrt{\frac{\varepsilon_g}{\varepsilon_0}} = e \sqrt{\frac{\mu_0}{\mu_g}} = e \sqrt{\frac{ Z_0}{\rho_g}} \

and these constants are the base units of the Stoney scale.

Primary Stoney units

Gravitational Stoney units

Stoney mass:

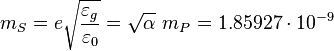m_S = e\sqrt{\frac{\varepsilon_g}{\varepsilon_0}} = \sqrt{\alpha} \ m_P = 1.85927\cdot 10^{-9} \

kg,

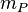where $m_P \$ is the Planck mass.

Stoney gravitational fine structure constant:

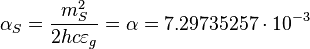\alpha_S = \frac{m_S^2}{2hc\varepsilon_g} = \alpha = 7.29735257 \cdot 10^{-3} \

Stoney fictitious gravitational torsion mass:

m_{\Omega} = \frac{h}{m_S} = 3.563801 \cdot 10^{-25} \

J s kg⁻¹.

Stoney scale gravitational torsion coupling constant: ^[3]

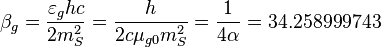$\beta_g = \frac {\varepsilon_g h c}{2 m_S^2} = \frac {h}{2c \mu_{g0} m_S^2} = \frac{1} {4\alpha} = 34.258999743 \$ .

Stoney gravitational impedance quantum:

R_{g} = \frac{ m_{\Omega}}{m_S} = \frac{h}{m_S^2} = 1.91677\cdot 10^{-16} \

J s kg⁻².

Electromagnetic Stoney units

Stoney charge:

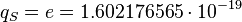q_S = e = 1.602176565 \cdot 10^{-19} \

Stoney electric fine structure constant:

\alpha_{S} = \frac{q_S^2}{2hc\,\varepsilon_0} = \alpha. \

Stoney fictitious magnetic charge:

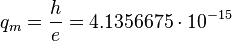q_m = \frac{h}{e} = 4.1356675\cdot 10^{-15} \

Wb.

Stoney scale magnetic coupling constant:

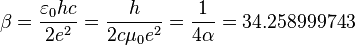\beta = \frac {\varepsilon_0 h c}{2 e^2} = \frac {h}{2c \mu_{0} e^2} = \frac{1} {4\alpha} = 34.258999743 \

Stoney electrodynamic impedance quantum:

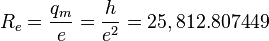R_{e} = \frac{ q_m }{e} = \frac{h}{e^2} = 25,812.807449 \

Ohm

which appears as the von Klitzing constant.

Secondary Stoney scale units

All systems of measurement feature is base units: in the International System of Units (SI), for example, the base unit of length is the meter. In the system of Stoney units, the Stoney base unit of length is known simply as the ‘’Stoney length’’, the base unit of time is the ‘’Stoney time’’, and so on. These units are derived from the presented above primary Stoney units, and arranged in Table 1 so as to cancel out the unwanted dimensions, leaving only the dimension appropriate to each unit. (Like all systems of natural units, Stoney units are an instance of dimensional analysis.)

The keys which are used in the Tables below: L = length, T = time, M = mass, Q = electric charge, Θ = temperature.

Table 1: Secondary Stoney units
Name	Dimension	Expressions	SI equivalent ^[4]
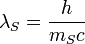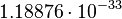Stoney wavelength	Length (L)	$\lambda_S = \frac{h}{m_Sc}$	$1.18876\cdot 10^{-33}$ m
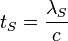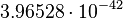Stoney time	Time (T)	$t_S = \frac{\lambda_S}{c}$	$3.96528\cdot 10^{-42}$ s
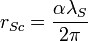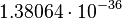Stoney classical radius	Length (L)	$r_{Sc} = \frac{\alpha \lambda_S}{2\pi}$	$1.38064\cdot 10^{-36}$ m
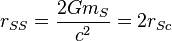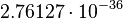Stoney Schwarzschild radius	Length (L)	$r_{SS} = \frac {2G m_S}{c^2}= 2 r_{Sc} \$	$2.76127\cdot 10^{-36}$ m
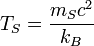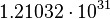Stoney temperature	Temperature (Θ)	$T_S = \frac{m_S c^2}{k_B}$	$1.21032\cdot 10^{31}$ K

Derived Stoney scale units

In any system of measurement, units for many physical quantities can be derived from base units. Table 2 offers a sample of derived Stoney units, some of which in fact are seldom used. As with the base units, their use is mostly confined to theoretical physics because most of them are too large or too small for empirical or practical use and there are large uncertainties in their values.

Table 2: Derived Stoney units

Name	Dimensions	Expression	SI equivalent
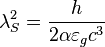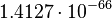Stoney area	Area (L²)	$\lambda_S^2 = \frac{h}{2\alpha \varepsilon_gc^3}$	$1.4127\cdot 10^{-66}$ m²
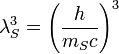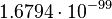Stoney volume	Volume (L³)	$\lambda_S^3 = \left(\frac{h}{m_Sc}\right)^3$	$1.6794\cdot 10^{-99}$ m³
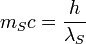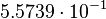Stoney momentum	Momentum (LMT⁻¹)	$m_S c = \frac{h}{\lambda_S}$	$5.5739\cdot 10^{-1}$ kg m/s
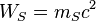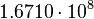Stoney energy	Energy (L²MT⁻²)	$W_S = m_S c^2 \$	$1.6710\cdot 10^{8}$ J
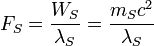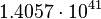Stoney force	Force (LMT⁻²)	$F_S = \frac{W_S}{\lambda_S} = \frac{m_Sc^2}{\lambda_S}$	$1.4057\cdot 10^{41}$ N
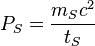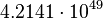Stoney power	Power (L²MT⁻³)	$P_S = \frac{m_S c^2 }{t_S}$	$4.2141\cdot 10^{49}$ W
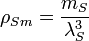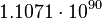Stoney density	Density (L⁻³M)	$\rho_{Sm} = \frac{m_S}{\lambda_S^3}$	$1.1071\cdot 10^{90}$ kg/m³
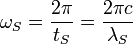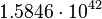Stoney angular frequency	Frequency (T⁻¹)	$\omega_S = \frac{2\pi}{t_S} = \frac{2\pi c}{\lambda_S}$	$1.5846\cdot 10^{42}$ rad s⁻¹
Stoney pressure	Pressure (L⁻¹MT⁻²)	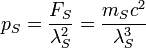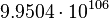$p_S = \frac{F_S}{\lambda_S^2} = \frac{m_Sc^2}{\lambda_S^3}$	$9.9504\cdot 10^{106}$ Pa
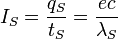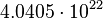Stoney current	Electric current (QT⁻¹)	$I_S = \frac{q_S}{t_S} = \frac{ec}{\lambda_S}$	$4.0405\cdot 10^{22}$ A
Stoney voltage	Voltage (L²MT⁻²Q⁻¹)	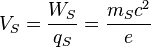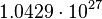$V_S = \frac{W_S}{q_S} = \frac{m_Sc^2}{e}$	$1.0429\cdot 10^{27}$ V
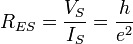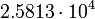Stoney electric impedance	Resistance (L²MT⁻¹Q⁻²)	$R_{ES} = \frac{V_S}{I_S} = \frac{h}{e^2}$	$2.5813\cdot 10^{4}$ Ohm
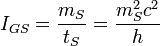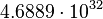Stoney gravitational current	Gravitational current (MT⁻¹)	$I_{GS} = \frac{m_S}{t_S} = \frac{m_S^2c^2}{h}$	$4.6889\cdot 10^{32}$ kg s⁻¹
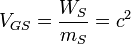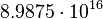Stoney gravitational potential	Gravitational potential (L²T⁻²)	$V_{GS} = \frac{W_S}{m_S} = c^2$	$8.9875\cdot 10^{16}$ m² s⁻²
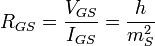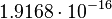Stoney gravitational impedance	Gravitational impedance (L²M⁻¹T⁻¹)	$R_{GS} = \frac{V_{GS}}{I_{GS}} = \frac{h}{m_S^2}$	$1.9168\cdot 10^{-16}$ m² kg⁻¹ s⁻¹
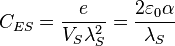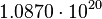Stoney electric capacitance per unit area	Electric capacitance (L⁻⁴M⁻¹T²Q²)	$C_{ES} = \frac {e}{ V_S \lambda_S^2 }= \frac{2 \varepsilon_0 \alpha}{\lambda_S}$	$1.0870\cdot 10^{20}$ F m⁻²
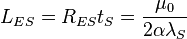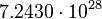Stoney electric inductance per unit area	Electric inductance (L²MQ⁻²)	$L_{ES} = R_{ES} t_S = \frac{\mu_0}{2 \alpha \lambda_S}$	$7.2430\cdot 10^{28}$ H m⁻²
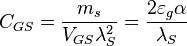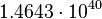Stoney gravitational capacitance per unit area	Gravitational capacitance (L⁻⁴MT² )	$C_{GS} = \frac {m_s}{ V_{GS}\lambda_S^2 }= \frac{2 \varepsilon_g \alpha}{\lambda_S}$	$1.4643\cdot 10^{40}$ m⁻⁴ kg s²
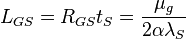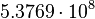Stoney gravitational inductance per unit area	Gravitational inductance (L²M⁻¹)	$L_{ GS } = R_{ GS } t_S = \frac{\mu_g}{2 \alpha \lambda_S}$	$5.3769\cdot 10^{8}$ m² kg⁻¹
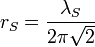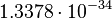Stoney particle radius	Length (L)	$r_S = \frac{\lambda_S}{2\pi \sqrt{2}}$	$1.3378\cdot 10^{-34}$ m
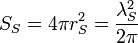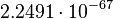Stoney particle area	Area (L²)	$S_S = 4\pi r_S^2 = \frac{\lambda_S^2}{2\pi}$	$2.2491\cdot 10^{-67}$ m²

Stoney scale forces

Stoney scale static forces

Electric Stoney scale force:

F_S(q_S, q_S) = \frac{1}{4\pi \varepsilon_0}\cdot \frac{e^2}{r^2} = \frac{\alpha \hbar c}{r^2}. \

Gravity Stoney scale force:

F_S(m_S, m_S) = \frac{1}{4\pi \varepsilon_g}\cdot \frac{m_S^2}{r^2} = \frac{\alpha_S \hbar c}{r^2}, \

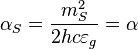where $\alpha_S = \frac{m_S^2}{2hc \varepsilon_g} = \alpha \$ is the gravitational fine structure constant.

Mixed (charge-mass interaction) Stoney force:

F_S(m_S, q_S) = \frac{1}{4\pi \sqrt{\varepsilon_g \varepsilon_0}}\cdot \frac{m_S\cdot e}{r^2} = \sqrt{\alpha_S \alpha}\frac{\hbar c}{r^2} = \frac{\alpha \hbar c}{r^2}. \

So, at the Stoney scale we have the equality of all static forces which describes interactions between charges and masses:

F_S(q_S, q_S) = F_S(m_S, m_S) = F_S(m_S, q_S) = \frac{\alpha \hbar c}{r^2}. \

Stoney scale dynamic forces

Magnetic Stoney scale force:

F_S(q_m, q_m) = \frac{1}{4\pi \mu_0}\cdot \frac{q_m^2}{r^2} = \frac{\beta \hbar c}{r^2}, \

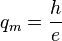where $q_m = \frac{h}{e}\$ is the fictitious elementary magnetic charge, 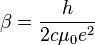$\beta = \frac{h}{2c\mu_0 e^2} \$ is the magnetic coupling constant.

Gravitational torsion force:

F_S(m_{\Omega}, m_{\Omega}) = \frac{1}{4\pi \mu_{g0}}\cdot \frac{ m_{\Omega}^2}{r^2} = \frac{\beta_g \hbar c}{r^2}, \

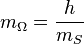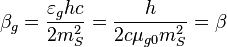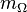where $m_{\Omega} = \frac{h}{m_S} \$ is the fictitious gravitational torsion mass, $\beta_g = \frac {\varepsilon_g h c}{2 m_S^2} = \frac {h}{2c \mu_{g0} m_S^2} =\beta \$ is the gravitational torsion coupling constant for the gravitational torsion mass $m_{\Omega } \$ .

Mixed dynamic (magnetic - torsion interaction) force:

F_S(q_m, m_{\Omega}) = \frac{1}{4\pi \sqrt{\mu_{g0} \mu_0}}\cdot \frac{ q_m \cdot m_{\Omega}}{r^2} = \sqrt{\beta_g \beta}\frac{\hbar c}{r^2} = \frac{\beta \hbar c}{r^2}. \

So, at the Stoney scale we have the equality of all dynamic forces which describes interactions between dynamic charges and masses:

F_S(q_m, q_m) = F_S(m_{\Omega}, m_{\Omega}) = F_S(q_m, m_{\Omega}) = \frac{\beta \hbar c}{r^2}. \

References

↑ 1.0 1.1 Stoney G. On The Physical Units of Nature, Phil.Mag. 11, 381–391, 1881
↑ J.G. O’Hara (1993). George Johnstone Stoney and the Conceptual Discovery of the Electron, Occasional Papers in Science and Technology, Royal Dublin Society 8, 5–28.
↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu
↑ Latest (2010) values of the constants

This article is issued from Wikiversity - version of the Thursday, November 06, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.