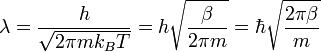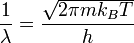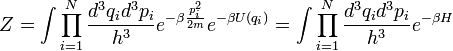Statistical mechanics

Statistical mechanics is a branch of mathematical physics that studies, using probability theory, the average behaviour of a mechanical system where the state of the system is uncertain. A common use of statistical mechanics is in explaining the thermodynamic behaviour of large systems.[1]


Thermal wavelength

\lambda = \frac{h}{\sqrt{2\pi m k_B T}} = h \sqrt{\frac{\beta}{2\pi m}}= \hbar \sqrt{\frac{2\pi\beta}{m}}
{1 \over \lambda} = \frac{\sqrt{2\pi m k_B T}}{h}

Partition function

Canonical: (in 3d)

Z = \int \prod_{i=1}^N \frac{d^3 q_i d^3 p_i}{h^3} e^{-\beta \frac{p_i^2}{2m}} e^{-\beta U(q_i)} = \int \prod_{i=1}^N \frac{d^3 q_i d^3 p_i}{h^3} e^{-\beta H}

See Also

  1. Classical thermodynamics
  2. Statistical thermodynamics
  3. Heat transfer


References

  1. ↑ Wikipedia:Statistical mechanics
This article is issued from Wikiversity - version of the Friday, December 27, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.