Spectroscopy/Vibrational spectroscopy
< Spectroscopy| | Subject classification: this is a chemistry resource . |
| | Resource type: this resource is a lesson. |
- Vibrational spectroscopy is to do with the oscillatory motion of atoms or groups within a molecule.
- It is relevant in the gas and condensed phases. We will only deal with gas phase vibrational spectroscopy.
- Vibrational motion at the molecule level is quantized in accordance with quantum mechanical theory.
- Transitions between discrete vibrational energy levels gives rise to the vibrational spectrum of the molecule.
- There are two main types of spectroscopy: Infrared and Raman.
We will study:
- classical vibrational motion, force constants, vibrational frequency
- quantum mechanical energy levels for the harmonic oscillator
- IR spectroscopy selection rules
- the anharmonic oscillator
- polyatomic molecules
- Raman spectroscopy
Classical vibrational motion
Classical vibrational motion is the periodic displacement of the atoms, leaving the centre of mass unmoved.
Consider a diatomic molecule as two atoms held together by a spring:
- Hooke's law says that the system undergoes simple harmonic motion - it experiences a restoring force proportional to its displacement x from equilibrium.
| Force: | Potential energy: |
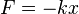 |
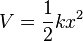 |
Vibrational energy levels
Solve the Schrödinger equation for the simple harmonic oscillator - it gives quantized energy levels Ev.
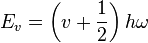 |
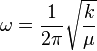 |
- EJ is measured in Joules
- v is the vibrational quantum number (= 0, 1, 2, ...)
- ω is the frequency of oscillation (measured in Hz)
| Converted to wavenumbers: | Vibrational constant: |
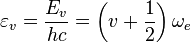 |
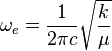 |
- The units of εv and ωe = cm-1
Gross selection rule
Gross Selection Rule: The requirement for a fluctuating dipole.
|
In other words, the dipole moment must change. |
When an infrared (IR) photon is absorbed by a molecular vibration, the dipole moment of the molecule must change when atoms are displaced relative to one another.
- Homonuclear diatomic molecules are IR inactive.
- Heteronuclear diatomic molecules are IR active.
|
Derivation for a diatomic molecule: For a transition to be allowed the transition dipole moment must be non-zero, i.e. Expanding
Neglecting higher terms, as bond extension tends to be small relative to bond length, it is clear that the first term is zero unless the initial and final states are the same i.e. there is no transition. When the initial and final states are not the same the first term is zero (the states are orthonormal). For the transition dipole moment to be non-zero the second term must be non-zero. For this to be true, the derivative of the dipole operator for the molecule with respect to internuclear separation must be non-zero. In other words there must be a change in dipole moment with a change in bond length. This argument is, strictly speaking, only applicable diatomics. |
Transitions between energy levels
Specific Selection Rule: The only transitions allowed are those which change the vibrational quantum number by 1 unit, i.e. Δv = ±1.
|
In other words, there can only be one transition at a time. |
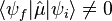 .
.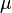 as a Taylor series about the equilibrium bond length,
as a Taylor series about the equilibrium bond length, 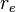 and by noting that
and by noting that 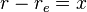 , this integral can be expanded as
, this integral can be expanded as