Exercises on the bisection method/Solution

Numerical analysis > Exercises on the bisection method/Solution

Exercise 1

• The following is a possible implementation of the bisection method with Octave/MATLAB:

function [x e iter]=bisection(f,a,b,err,itermax)
%The function bisection find the zeros of function
%with the bisection algorithm.
%It returns the zero x, the error e, and the number of iteration needed iter
%
%HOW TO USE IT:
%Example
%>>f=@(x)x.^3;
%>>a=-1; b=2;
%>>err=1e-5; itermax=1000;
%>>[x e iter]=bisection(f,a,b,err,itermax);

e=b-a;
iter=0;
fa=f(a);
if( fa .* f(b) >= 0 ) 
	x =[];
	disp("f(a) *  f(b) >= 0! No solution!")
else
	while( e > err )
		iter = iter + 1;
		x = 0.5 * ( b + a )
		e = abs(b - x);
		fx = f(x);
		if( fx == 0 )
			break;
		elseif( fx * fa > 0 )
			a = x;
			fa = fx;
		else
			b = x;
		end
		if( iter == itermax)
			break;
		end	
	end
end

• The solution of the points 1, 2 e 3 can be found in the example of the bisection method.

For point 4 we have

,

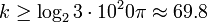so we would need at least 70 iterations. The chance of convergence with such a small precision depends on the calculatord: in particular, with Octave, the machine precision is roughly 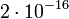. For this reason it does not make sense to choose a smaller precision. The number of iterations, if we don't specify a maximum number, would be infinite.

Exercise 2

1. To verify the existence of a root 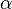we need to show that the hypothesis roots theorem are satisfied. The first hypothesis requires to be continuous. Obviosly this is a continuous function since it is sum of two continuous functions. The second hypotheses requires the function to have oppiste signs at the interval extrema, and in fact we find

   .

   

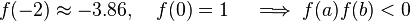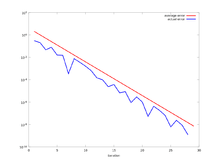   Comparison of the average and actual errors computed with the bisection method in logarithmic scale..

   To show the uniqueness of the root we need to prove that the function is monotone and in fact

   .

2. The number of iterations need is given by

   ,

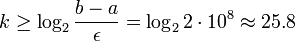   and so we have .

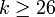3. The interval does not contain aany root as the second hypotesis of the roots theorem fails, in fact

   .

4. 
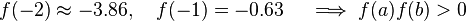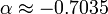
5. In the plot we show in red the average errorand in blu the actual error. From the graph, it is clear that the actual error is not a monotone function. Moreover, note that the global behavior of both curves is the same, clarifying the term average error for .

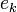Exercise 3

For the solution look at the convergence analysis in the bisection method page.