Sole sufficient operator

☞ This page belongs to resource collections on Logic and Inquiry.

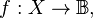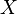A sole sufficient operator is an operator that is sufficient by itself to generate every operator in a specified class of operators. In the context of logic, it is a logical operator that suffices to generate every boolean-valued function, $f : X \to \mathbb{B},\!$ where $X\!$ is an arbitrary set and where 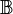$\mathbb{B}\!$ is a generic two-element set, typically 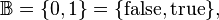$\mathbb{B} = \{ 0, 1 \} = \{ \mathrm{false}, \mathrm{true} \},\!$ in particular, to generate every finitary boolean function,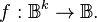 $f : \mathbb{B}^k \to \mathbb{B}.\!$

Syllabus

Focal nodes

Peer nodes

Logical operators

Relational concepts

Information, Inquiry

Document history

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

This article is issued from Wikiversity - version of the Saturday, November 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.