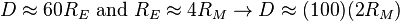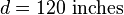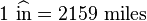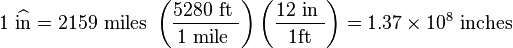Skygazing/Solar eclipse lab on a sunny day

Purpose

Today we did a lab that creates a scale model of a solar eclipse. In his left hand is an iPhone that can take the shadow's photograph.

Is this shadow of the 1-inch ball the umbra or the penumbra?^[1] The vertical shadow is the support that held the Styrofoam ball in place.^[2]

A 1-inch diameter "Moon" must be held 110 inches above the ground for a proper scale model^[3]

The digital image of the penumbra was imported into Inkscape ^[4] and converted into grey-scale objects. A map of USA was found on commons and placed next to it at the proper scale. This evidence suggests that the penumbra associated with a solar eclipse is larger than the United States.

To measure the size of the Moon's penumbra during a solar eclipse using a scale model.

Why this is a scale model

A scale model is a drawing that preserves all the angles. Here we represent the Moon as a small Styrofoam ball. The Earth is most easily represented as a map of a region where a solar eclipse is expected. Here we use the United States.

For the Sun, we use the actual object, which of course is not to the same scale. But for our purposes, any object that produces light with the proper angular distribution can be used. In other words, the actual Sun provides the required angular spread of light rays (i.e., light spread over a range of about half a degree). The actual size of the Sun is irrelevant (otherwise one could use a solar eclipse to calculate the size and distance to the Sun).

Equipment

10 ft rod to hold up the model "Moon" (we clamped a two-meter stick to a one-meter stick)
One inch diameter ball to server as the Moon (rod and ball dimensions may vary proportionally)
Tape measure or other way to measure distance on the ground (we used 2 metersticks)
Camera (we used an Apple iPhone)
White screen. We used about a dozen sheets of paper. It would also be worthwhile to print onto this paper a properly scaled image of a region on Earth, or perhaps the Earth itself.
At least two people (three works better)
The Sun on a sunny day
The instructor and students should be mentally prepared to do calculations and proportional reasoning on three different scales:

The solar system (especially Earth/Moon system)
A scale where the Moon is reduced to a small ball
A scale on which photos of the shadow are analyzed

Procedure

The Moon was a one inch diameter styrofoam ball attached to a stick that was 110 inches long (chosen to match the Earth-Moon distance).
We forgot to measure the altitude of the Sun. Fortunately the images on commons contain a time stamp and we know where we were (Celina, Ohio). Somewhere a website will give us that angle.
Photograph the shadow alongside a ruler for scale.
Record the location of the shadow so that you may later calculate the distance from the "Moon" at the end of the stick and the "Earth", represented by the white paper on the ground.

How far from the model "Earth" should we hold the model "Moon"?

The Moon is about 60 earth-radii from Earth.
The Moon has a diameter about 1/4 that of the Earth.
Our Styrofoam "Moon" had a diameter of one inch.

Keeping track of scaled objects can be confusing. One trick is to use capital letters for the real thing and lower case for the scale:

d

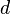equals scaled distance from Earth to Moon

D

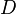is the actual distance.

r_E

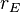equals scaled radius of Earth

R_E

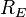is the actual radius.

r_M

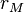equals scaled radius of the Moon

R_M

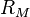is the actual radius.

Focusing on only astronomical data, we have:

D \approx 60 R_E \text{ and } R_E \approx 4 R_M \rightarrow D \approx (100)(2 R_M)

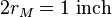Since $2r_M=1\text{ inch}$ we conclude that the Styrofoam ball should be held at a distance of

d = 120\text{ inches}

away from the Earth. Our "model" Earth was just a piece of paper, but we can add a scale to it using the fact that a one inch diameter ball represents the 2159 mile diameter Moon.

Calculating the scale

The scale is:

1 \ \widehat\text{in} = 2159\text{ miles }

where we have used the "hat" notation to define the "scaled" inch. This "scaled" inch equals 2159 miles, but is also one (actual) inch on the scale model.

1 \ \widehat\text{in} = 2159\text{ miles } \left(\frac{ 5280 \ \text{ft } }{1 \text{ mile }}\right) \left(\frac{ 12 \ \text{in } }{1 \text{ft}}\right) = 1.37 \times 10^8 \text{ inches}

In other words, our scale is 1.37 x 10⁸ to 1.

Scaling the USA

http://www.distance.to/New-York/San-Francisco says that the distance between NYC and SF is 2566 miles = 1430 km. Convert this to centimeters and divide by the scaling factor to get:

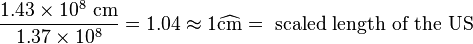
$\frac {1.43\times 10^8 \text{ cm}} {1.37 \times 10^8} =1.04 \approx 1\widehat\text{cm} = \text{ scaled length of the US}$

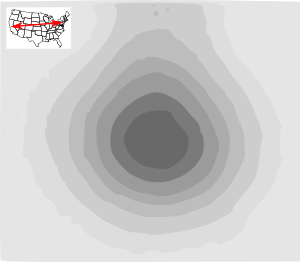
This says that the penumbra is larger than the USA? This seems to big, but see below. This experiment should be repeated and the results reported here.

Other photos from the experience

showing how we did the lab

photos of shadow

300 cm
250 cm
200 cm
150 cm
100 cm
50 cm
0 cm

Understanding the size of the penumbra

This diagram explains why the penumbra of a solar eclipse is approximately twice the size of the Moon. Since the Sun and Moon have nearly the same angular diameter, the umbra is reduced to nearly a single point in length. Therefore the three angles marked in red are nearly equal, all with a base equal to the Moon's diameter.

Conclusion

If you go here http://eclipse.gsfc.nasa.gov/SEgoogle/SEgoogle2001/SE2017Aug21Tgoogle.html, you will see that the penumbra is very large and extends far outside the USA. Perhaps our results are correct.

We measured the length of the shadow on the photograph marked 0cm. It was projected on a classroom screen at a scale where 4.9 cm* equals 1 cm. In other words, the classroom projected image of the photo expanded the meter stick so that 1 cm on the stick measured 4.9cm* on the screen.^[5]. The shadow's length on the screen was 21 plus/minus 1 cm*. We concluded that the umbra was

1.69 ± 0.08 inches^[6]

This much smaller than the 2 inch umbra we expected from a 1 inch moon. Perhaps the brightest part of the penumbra was indistinguishable from the illuminated portion of the paper.^[7]

References and footnotes

↑ It is almost entirely penumbra because the ball was held so that the angular size of the ball nearly equaled the angular size of the Sun. If the two angular sizes are equal, the umbra is essentially reduced to the area of a single point.
↑ We use a ballpoint pen that was rammed into the Styrofoam ball to hold it in place.
↑ Although our calculation stipulated a 120 inch rod, a more careful calculation indicated that 111 inches was closer to the condition that the angular size of the Styrofoam ball equals the angular size of the Moon.
↑ People interested in editing for Wikipedia should know about Inkscape because it is open source and makes the editable svg files preferred by Wikipedia and its "sisters".
↑ Here the asterisk indicates that the cm* was as measured on a screen projected in the classroom. This forms a third scale. In this context, cm refers to the actual photograph.
↑ More properly, this shadow was 1.69 hat-inches, since the hat is used on measurement made on the scale model.
↑ Another factor is that the student was not instructed to try for the largest possible shadow. After class, the instructor could discern a faint shadow 30 cm* in length on the screen that projected the image.

This article is issued from Wikiversity - version of the Monday, April 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.