Shifted inverse iteration
We can apply the w:power method to find the largest eigenvalue and the w:inverse power method to find the smallest eigenvalue of a given matrix.We can also find the middle eigenvalue by the shifted inverse power method. Before explaining this method, I'd like to introduce some theorems which are very necessary to understand it.
Background Theorems
(See http://www.math.nuk.edu.tw/jinnliu/Software_Engineering/IS_PowerMethod.pdf)
Suppose that λ and a nonzero vector V are an eigenpair of A. If α is any constant, then λ- α and V are an eigenpair of the matrix.
Suppose that λ and a nonzero vector V are an eigenpair of A. If λ is not equal to α, then 1/(λ -α) and V are an eigenpair of the matrix.
Shifted inverse power method
Assume that the n×n matrix A has distinct w:eigenvalues
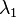 ,
, 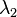 ,....
,....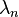 and consider the eigenvalue
and consider the eigenvalue
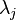 .
Then a constant α can be chosen so that
.
Then a constant α can be chosen so that
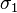 =1 / (
=1 / (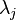 - α)
- α)
is the dominant eigenvalue of
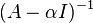 .
Furthermore, if
.
Furthermore, if
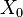 is chosen appropriately which is the initial guess vector, then the sequences
is chosen appropriately which is the initial guess vector, then the sequences
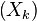 defined by
defined by
and 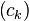 defined by
defined by
will converge to the dominant eigenpair
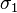 ,
,
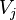 of the matrix
of the matrix
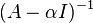 .
Therefore, the corresponding eigenvalue for the matrix A is given by
.
Therefore, the corresponding eigenvalue for the matrix A is given by
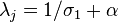 .
.
Example
Use the shifted inverse power method to find the eigenpairs of the matrix
![A=\left[\begin{array}{c c c}0 & 11 & -5 \\-2 & 17 & -7 \\-4 & 26 & -10 \end{array} \right]](../I/m/f6d3a914ed491e4e46ae227fe3c0acc5.png) .
.
Use the fact that the eigenvalues of A are
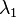 =4,
=4,
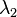 =2,
=2,
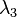 =1,
and select an appropriate α and starting vector for each case.
=1,
and select an appropriate α and starting vector for each case.
Case1: For the eigenvalue
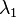 =4,
we select α=4.2 and the starting vector
=4,
we select α=4.2 and the starting vector
![X_0=\left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right]](../I/m/e9c9aa94a73ad3c38f89cdab884e4948.png) .
.
First we can get
![(A - 4.2 I)= \left[\begin{array}{c c c}-4.2 & 11 & -5 \\-2 & 12.8 & -7 \\-4 & 26 & -14.2 \end{array} \right]](../I/m/a271270c3b42abf2e1e96153d5bd037d.png)
and then we can apply the shifted inverse power method
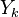 =
=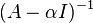
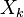 .
.
Therefore,
![\left[\begin{array}{c c c}-4.2 & 11 & -5 \\-2 & 12.8 & -7 \\-4 & 26 & -14.2 \end{array} \right]](../I/m/a88c7299b8d15d67fbf98df4d04289b7.png)
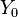 =
= ![X_0=\left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right]](../I/m/e9c9aa94a73ad3c38f89cdab884e4948.png) .
.
Solving this system of equations, we get
![Y_0=\left[\begin{array}{c}-9.545454545 \\-14.09090909 \\ -23.18181818 \\\end{array} \right]](../I/m/26ee97322a6626d691c02d3a6fa23550.png) .
.
Next we can compute
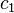 =
=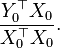 ,
,
so
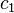 =-15.606060605.
Since
=-15.606060605.
Since
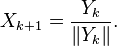 ,
,
it implies
![X_1=\left[\begin{array}{c}-0.4117 \\-0.6078 \\ -1 \\\end{array} \right]](../I/m/a4ade1e5a789d2deba4aa639f9081ce9.png) .
.
We continue doing the second iteration:
![\left[\begin{array}{c c c}-4.2 & 11 & -5 \\-2 & 12.8 & -7 \\-4 & 26 & -14.2 \end{array} \right]](../I/m/a88c7299b8d15d67fbf98df4d04289b7.png)
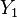 =
= ![X_1=\left[\begin{array}{c}-0.4117 \\-0.6078 \\ -1 \\\end{array} \right]](../I/m/a4ade1e5a789d2deba4aa639f9081ce9.png) .
.
Thus
![Y_1=\left[\begin{array}{c}2.14795 \\3.21746 \\ 5.35650 \\\end{array} \right]](../I/m/26aaf931bfe4516b5e61874af393ee7b.png) .
.
It implies
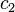 =-5.326069
and
=-5.326069
and
![X_2=\left[\begin{array}{c}0.400998 \\0.600665 \\ 1 \\\end{array} \right]](../I/m/081f354fe33a176e5f87182ec7085850.png) .
.
We should continue the iteration and finally we got the sequence
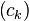 will converge to
will converge to
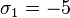 ,
which is the dominant eigenvalue of
,
which is the dominant eigenvalue of
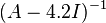 ,
and the sequences
,
and the sequences
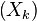 converges to
converges to
![V_1=\left[\begin{array}{c}0.4 \\0.6 \\ 1 \\\end{array} \right]](../I/m/34105a32e34f77b176bf8bc524859e6d.png)
after 9 iterations. We can get the eigenvalue
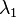 of A by the formula:
of A by the formula:
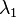 = 1 /
= 1 / 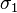 + α= 1/(-5) + 4.2 =4.
+ α= 1/(-5) + 4.2 =4.
We can apply the same approach to find another two eigenvalues of the given matrix A.
Exercise
Use the shifted inverse power method to find the eigenvalue
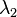 =2
=2
for the same matrix A as the example above, given the starting vector
![X_0=\left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right]](../I/m/e9c9aa94a73ad3c38f89cdab884e4948.png) ,
,
α=2.1.
Solution:
For the eigenvalue
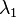 =2,
=2,
we select α=2.1 and the starting vector
![X_0=\left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right]](../I/m/e9c9aa94a73ad3c38f89cdab884e4948.png) .
.
First we can get
![(A - 2.1 I)= \left[\begin{array}{c c c}-2.1 & 11 & -5 \\-2 & 14.9 & -7 \\-4 & 26 & -12.1 \end{array} \right]](../I/m/2509cdf8696ceafd43c7abfd78857bd2.png) .
.
Therefore,
![\left[\begin{array}{c c c}-2.1 & 11 & -5 \\-2 & 14.9 & -7 \\-4 & 26 & -12.1 \end{array} \right]](../I/m/4a70e4045f99c58ddb223d04f5c1c6ab.png)
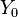 =
= ![X_0=\left[\begin{array}{c}1 \\1 \\ 1 \\\end{array} \right]](../I/m/e9c9aa94a73ad3c38f89cdab884e4948.png) .
.
So
![Y_0=\left[\begin{array}{c}11.05263158 \\21.57894737 \\ 42.63157895 \\\end{array} \right]](../I/m/737e1c6e39a160bf9fbe9b0466d2c4e9.png)
and
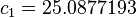
It implies
![X_1=\left[\begin{array}{c}0.2592592593 \\0.5061728395 \\ 1 \\\end{array} \right]](../I/m/20f7270c1baec63b90b0447250d8e274.png) .
.
After 7 iterations,we got
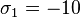
and
![V_1=\left[\begin{array}{c}0.25 \\0.5 \\ 1 \\\end{array} \right]](../I/m/7c5a0a2574dc77a6c9c7ce52575ae6bc.png) .
.
Doing some computation, We got
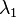 = 1 /
= 1 / 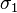 + α= 1/(-10) + 2.1 =2.
+ α= 1/(-10) + 2.1 =2.
Exercise
Use w:Matlab to do the shifted inverse power method to find the eigenvalue
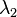 =5.1433
for the given matrix
=5.1433
for the given matrix
![A=\left[\begin{array}{c c c}6 &2 & -1 \\2 & 5 & 1 \\-1 & 1 & 4 \end{array} \right]](../I/m/90d9e153d0b737c255f3bb9d1ec4fe10.png) .
.
The starting vector is
![X_0=\left[\begin{array}{c}1 \\1 \\ 3 \\\end{array} \right]](../I/m/9a8dbb96396366d0dbb45f7aac2a463e.png) ,
,
α=6.
Solution:
First we can get
![(A - 6 I)= \left[\begin{array}{c c c}0 & 2 & -1 \\2 & -1 & 1 \\-1 & 1 & -2 \end{array} \right]](../I/m/cc897006f2d6a0c02169e8b758ba3437.png) .
.
Then we can apply the method mentioned above to find the middle eigenvalue of the matrix. Below is the Matlab code for this question.
for i=1:7 y=linsolve(A,x); e=(y'*x)/(x'*x); x=y/norm(y); end
We can find that the sequence
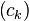 will converge to
will converge to
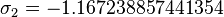 after 7 iterations.
Doing some computation, We got
after 7 iterations.
Doing some computation, We got
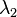 = 1 /
= 1 / 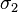 + α= 1/(-1.167238857441354) + 6 = 5.143277321839636
+ α= 1/(-1.167238857441354) + 6 = 5.143277321839636
which is approximately equal to 5.1433, the middle eigenvalue of the matrix.
Reference
Yu-Kai Hong,An introduction to the Power Method and (shifted/Inverse) Power Method,2007
John H.Mathews,Kurtis D.Fink,Numerical method using Matlab,4th edition,2004
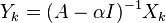
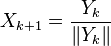
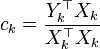 (
(