Set theory

Resource type: this resource is a lesson.

Basic Definition

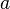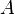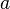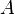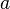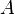Intuitively, a set can be thought as a well-defined collection of objects. In set theory, we use the word element to refer to these objects. We usually use capital letters for the sets and small letters for the elements. If an element, say $a$ , belongs to a set $A$ , we say that " $a$ is a member of the set $A$ ", or we could also say that " $a$ is in $A$ ", and we denote this by writing 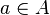$a \in A$ . Similarly, if 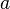$a$ is not in 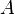$A$ , we would write 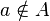$a \notin A$ . You have probably seen this already, for example when we write 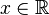$x \in \mathbb{R}$ . In this case, 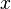$x$ is the element and 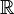$\mathbb{R}$ is the set, namely the set of the real numbers.

There are two ways that we could show which elements are members of a set: by listing all the elements, or by specifying a rule which leaves no room for misinterpretation. In both ways we will use curly braces to enclose the elements of a set. Say we have a set 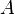$A$ that contains all the positive integers that are smaller than ten. In this case we would write 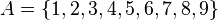$A = \{1,2,3,4,5,6,7,8,9\}$ . 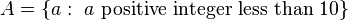We could also use a rule to show the elements of this set, as in $A = \{a:\text{ }a\text{ positive integer less than 10}\}$ .

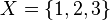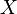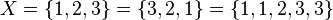In a set, the order of the elements is irrelevant, as is the possibility of duplicate elements. For example, we write $X = \{ 1, 2, 3 \}$ to denote a set $X$ containing the numbers 1, 2 and 3. Or, $X = \{ 1, 2, 3 \} = \{3,2,1 \} = \{1,1,2,3,3\}$ .

Learning resources

Wikiversity

Introduction_to_set_theory/Lecture_1

Wikipedia

Set theory category

This article is issued from Wikiversity - version of the Monday, October 14, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.