Separation of variables method

Resource type: this resource contains a lecture or lecture notes.

Introduction

We often consider partial differential equations such as

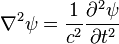$\nabla^2 \psi = \frac{1}{c^2} \frac{\partial^2 \psi}{\partial t^2}$ ,

which is recognisable as the wave equation in three dimensions, with 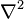$\nabla^2$ being the Laplacian operator, 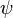$\psi$ being some function of three spacial dimensions and time, and c being the speed of the wave.

These are often found by considering the physical connotations of a system, but how can we find a form of 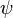$\psi$ such that the equation is true?

Finding General Solutions

One way of doing this is to make the assumption that 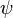$\psi$ itself is a product of several other functions, each of which is itself a function of only one variable. In the case of the wave equation shown above, we make the assumption that

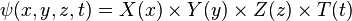
$\psi(x, y, z, t) = X(x) \times Y(y) \times Z(z) \times T(t)$

(NB Remember that the upper case characters are functions of the variables denoted by their lower case counterparts, not the variables themselves)

By substituting this form of 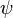$\psi$ into the original wave equation and using the three dimensional cartesian form of the Laplacian operator, we find that

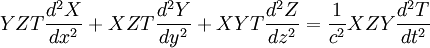
$YZT \frac{d^2X}{dx^2} + XZT \frac{d^2Y}{dy^2} + XYT \frac{d^2Z}{dz^2} = \frac{1}{c^2} XZY \frac{d^2T}{dt^2}$

We can then divide this equation through by $\psi$ to produce the following equation:

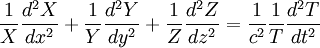
$\frac{1}{X} \frac{d^2X}{dx^2} + \frac{1}{Y} \frac{d^2Y}{dy^2} + \frac{1}{Z} \frac{d^2Z}{dz^2} = \frac{1}{c^2} \frac{1}{T} \frac{d^2T}{dt^2}$

Both sides of this equation must be equal for all values of x, y, z and t. This can only be true if both sides are equal to a constant, which can be chosen for convenience, and in this case is -(k²).

The time-dependent part of this equation now becomes an ordinary differential equation of form

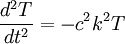
$\frac{d^2T}{dt^2} = -c^2k^2T$

This is easily soluble, with general solution

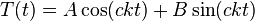
$T(t) = A \cos(ckt) + B \sin(ckt)$

with A and B being arbitrary constants, which are defined by the specific boundary conditions of the physical system. Note that the key to finding the time-dependent part of the original function was to find an ODE in terms of time. This general process of finding ODEs from PDEs is the essence of this method.

This article is issued from Wikiversity - version of the Monday, June 18, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.