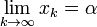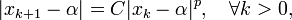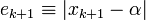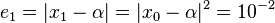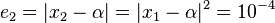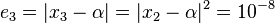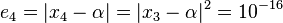Rootfinding for nonlinear equations

Rootfinding for nonlinear equations

Numerical analysis > Rootfinding for nonlinear equations

Here we want to solve an equation of the kind 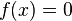$f(x)=0$ .

Suppose that there exist 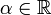$\alpha \in \mathbb{R}$ such that 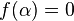$f(\alpha)=0$ . Then we want to construct a sequence 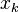$x_k$ , with 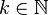$k \in \mathbb{N}$ , such that

\lim_{k\to\infty}x_k=\alpha

The number 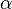$\alpha$ is called root (of the function $f$ ).

Convergence

If the sequence defined by the numerical method converges, we can ask what the rate of convergence is. With this aim, we define the order of convergence of a sequence :

Definition (Order of convergence). A sequence 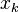$x_k$ converges to 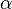$\alpha$ with order 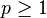$p\geq 1$ if

|x_{k+1}-\alpha | = C|x_{k}-\alpha |^p, \quad \forall k>0,

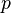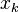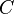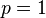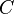$p$ is the order of convergence of the numerical method that has generated the sequence $x_k$ . The constant $C$ is called rate of convergence. If $p=1$ and $C$ is between 0 and 1, the convergence is said to be linear convergence.Under the linear convergence condition,if 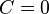$C=0$ , the sequence is said to converge superlinearly and if 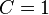$C=1$ , then the sequence is said to converge sublinearly.

The quantity

e_{k+1}\equiv |x_{k+1}-\alpha |

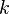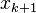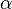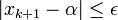represents the error at step $k$ . In general, with a numerical method, we do a finite number of iterations and for this reason we seek only an approximation $x_{k+1}$ of the true root $\alpha$ . In particular, we can define a tolerance $\epsilon$ such that if $|x_{k+1}-\alpha|\leq\epsilon$ ,we can stop the iteration and conclude that 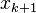$x_{k+1}$ is the approximation of the true root.

Example

Suppose that the sequence 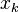$x_k$ converges to 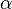$\alpha$ with order 2, where the constant 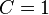$C=1$ , and suppose that the initial error 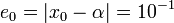$e_0 = |x_0-\alpha|=10^{-1}$ . Consider a tolerance 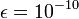$\epsilon = 10^{-10}$ , then we can find the approximation of the true root by using the definition of convergence.Hence,

e_1 = |x_1-\alpha|=|x_0-\alpha |^2=10^{-2}

which is greater than the tolerance, so we should keep going until the error is less than the tolerance. We can get

e_2 = |x_2-\alpha|=|x_1-\alpha |^2=10^{-4}

which is also greater than the tolerance, thus we should do the iteration to calculate

e_3 = |x_3-\alpha|=|x_2-\alpha |^2=10^{-8}

which is still larger than the tolerance. Similarly,

e_4 = |x_4-\alpha|=|x_3-\alpha |^2=10^{-16}

which is less than the tolerance. Therefore, we can stop here and can conclude that 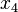$x_4$ is the approximation of the true root.

YangOu (talk) 02:44, 26 October 2012 (UTC)

This article is issued from Wikiversity - version of the Friday, October 26, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.