Quizbank/Calculus Physics/T1study
< Quizbank < Calculus PhysicsCalcPhysIIT1_Study
If you are reading this as a Wikiversity page, proper pagebreaks should result if printed using your browser's print option. On Chrome, Explorer, and Firefox, this option is available in the upper right hand corner of your screen. But, pagebreaks do not render properly if you use "Printable version" on Wikiversity's Print/export option on the left-hand sidebar.
- This document contains either a study guide OR pairs of exams taken from the same exam bank
- If two exams have the same s-number, then v1 and v2 have the same questions, presented in different (random) order.
- Exams with different s-numbers have different questions and may not have the same difficulty.
- Click items in the table of contents and appropriate page should be reached. This feature should allow you to print only those pages that you need.
- At the end of this document
- Attribution for the quizzes identifies where the questions were obtained
- Study guide links reading materials and/or relevant equations.
CalcPhysIIT1_Study-v1s1
1. Integrate the line integral of, 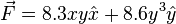 , along the y axis from y = 4 to y = 16
, along the y axis from y = 4 to y = 16
- ___ a) 1.31E+05
- ___ b) 1.40E+05
- ___ c) 1.50E+05
- ___ d) 1.61E+05
- ___ e) 1.72E+05
2. Integrate the function, 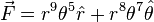 , along the first quadrant of a circle of radius 4
, along the first quadrant of a circle of radius 4
- ___ a) 1.14E+06
- ___ b) 1.21E+06
- ___ c) 1.30E+06
- ___ d) 1.39E+06
- ___ e) 1.49E+06
3. Integrate the line integral of 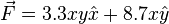 from the origin to the point at x = 2.1 and y = 3.2
from the origin to the point at x = 2.1 and y = 3.2
- ___ a) 4.18E+01
- ___ b) 4.48E+01
- ___ c) 4.79E+01
- ___ d) 5.12E+01
- ___ e) 5.48E+01
4. Integrate the function, 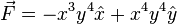 , as a line integral around a unit square with corners at (0,0),(1,0),(1,1),(0,1). Orient the path so its direction is out of the paper by the right hand rule
, as a line integral around a unit square with corners at (0,0),(1,0),(1,1),(0,1). Orient the path so its direction is out of the paper by the right hand rule
- ___ a) 3.43E-01
- ___ b) 3.67E-01
- ___ c) 3.93E-01
- ___ d) 4.21E-01
- ___ e) 4.50E-01
5. What is the magnitude of the electric field at the origin if a 3.1 nC charge is placed at x = 6.2 m, and a 2.6 nC charge is placed at y = 6 m?
- ___a) 5.47 x 10-1N/C
- ___b) 6.32 x 10-1N/C
- ___c) 7.3 x 10-1N/C
- ___d) 8.43 x 10-1N/C
- ___e) 9.73 x 10-1N/C
6. What angle does the electric field at the origin make with the x-axis if a 2 nC charge is placed at x = -8 m, and a 1.4 nC charge is placed at y = -9.3 m?
- ___a) 2.37 x 101degrees
- ___b) 2.74 x 101degrees
- ___c) 3.16 x 101degrees
- ___d) 3.65 x 101degrees
- ___e) 4.22 x 101degrees
7. A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the x component of the electric field at (x,y) =( 4a, 2a) is βkQ/a2, where β equals
- ___a) 7.31 x 10-3 unit
- ___b) 8.86 x 10-3 unit
- ___c) 1.07 x 10-2 unit
- ___d) 1.3 x 10-2 unit
- ___e) 1.57 x 10-2 unit
8. A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the y component of the electric field at (x,y) =( 1.1a, 1.2a) is βkQ/a2, where β equals
- ___a) 2.36 x 10-1 unit
- ___b) 2.86 x 10-1 unit
- ___c) 3.47 x 10-1 unit
- ___d) 4.2 x 10-1 unit
- ___e) 5.09 x 10-1 unit
9. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 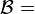
- ___ a) −7
- ___ b) 3
- ___ c) −3
- ___ d) −3
- ___ e) 2
10. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 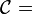 :
:
- ___ a) s−4
- ___ b) 5−s
- ___ c) 1−s
- ___ d) s−1
- ___ e) 5
11. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 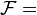 :
:
- ___ a) 3/2
- ___ b) 1/2
- ___ c) 3
- ___ d) 2
- ___ e) 2/3
12. A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 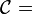 :
:
- ___ a) s−7
- ___ b) 8
- ___ c) 3−s
- ___ d) 7−s
- ___ e) s−3
13. A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 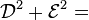 :
:
- ___ a) 32 + 82
- ___ b) (7-s)2 + 82
- ___ c) 72 + (8−s)2
- ___ d) 72 + (3−s)2
- ___ e) 72 + 82
14. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 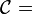
- ___ a) s−7
- ___ b) s−3
- ___ c) 3
- ___ d) 7−s
- ___ e) 3−s
15. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where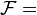
- ___ a) 2
- ___ b) 1/2
- ___ c) 3/2
- ___ d) 3
16. A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
 (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 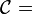 :
:
- ___ a) s − 9
- ___ b) 2
- ___ c) 9 − s
- ___ d) 2 − s
- ___ e) s − 2
17. A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
 (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 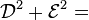 :
:
- ___ a) 92 + (2-s)2
- ___ b) 92 + (7-s)2
- ___ c) 72 + (2-s)2
- ___ d) 22 + (9-s)2
- ___ e) 22 + (7-s)2
18. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 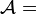 :
:
- ___ a) 1/2
- ___ b) 2
- ___ c) 8
- ___ d) 4
19. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 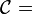 :
:
- ___ a) 4
- ___ b) s−4
- ___ c) 8−s
- ___ d) 4−s
- ___ e) s−8
20. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the x component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 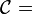 :
:
- ___ a) s−4
- ___ b) 8−s
- ___ c) s−8
- ___ d) 4
- ___ e) 4−s
21. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the x component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 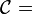 :
:
- ___ a) s−4
- ___ b) s−1
- ___ c) 1−s
- ___ d) 5−s
- ___ e) 5
22. A cylinder of radius, R, and height H has a uniform charge density of 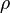 . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
. The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
- ___ a)c)
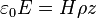
- ___ b)d) none of these are correct
- ___ c)e)
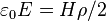
- ___ d)
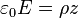
- ___ e)b)
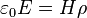
23. A cylinder of radius, R, and height H has a uniform charge density of 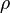 . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
. The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
- ___ a)b) none of these are correct
- ___ b)e)
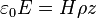
- ___ c)d)
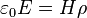
- ___ d)c)
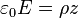
- ___ e)
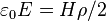
24. A sphere has a uniform charge density of 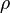 , and a radius or R. What formula describes the electric field at a distance r > R?
, and a radius or R. What formula describes the electric field at a distance r > R?
- ___ a) none of these are correct
- ___ b)d)
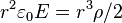
- ___ c)e)

- ___ d)c)
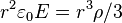
- ___ e)b)

25. A sphere has a uniform charge density of 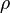 , and a radius equal to R. What formula describes the electric field at a distance r < R?
, and a radius equal to R. What formula describes the electric field at a distance r < R?
- ___ a)
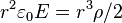
- ___ b)b)

- ___ c)d)
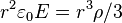
- ___ d)c) none of these are correct
- ___ e)e)

26. A cylinder of radius, R, and height H has a uniform charge density of 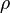 . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
. The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
- ___ a)b)
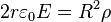
- ___ b)d) none of these are correct
- ___ c)
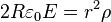
- ___ d)c)
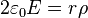
- ___ e)e)
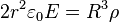
27. A cylinder of radius, R, and height H has a uniform charge density of 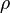 . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
. The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
- ___ a)
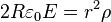
- ___ b)b)
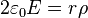
- ___ c)c)
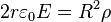
- ___ d)e)
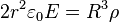
- ___ e)d) none of these are correct
Key to CalcPhysIIT1_Study-v1s1
1. Integrate the line integral of, 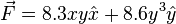 , along the y axis from y = 4 to y = 16
, along the y axis from y = 4 to y = 16
- - a) 1.31E+05
- + b) 1.40E+05
- - c) 1.50E+05
- - d) 1.61E+05
- - e) 1.72E+05
2. Integrate the function, 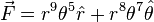 , along the first quadrant of a circle of radius 4
, along the first quadrant of a circle of radius 4
- - a) 1.14E+06
- + b) 1.21E+06
- - c) 1.30E+06
- - d) 1.39E+06
- - e) 1.49E+06
3. Integrate the line integral of 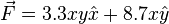 from the origin to the point at x = 2.1 and y = 3.2
from the origin to the point at x = 2.1 and y = 3.2
- - a) 4.18E+01
- + b) 4.48E+01
- - c) 4.79E+01
- - d) 5.12E+01
- - e) 5.48E+01
4. Integrate the function, 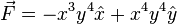 , as a line integral around a unit square with corners at (0,0),(1,0),(1,1),(0,1). Orient the path so its direction is out of the paper by the right hand rule
, as a line integral around a unit square with corners at (0,0),(1,0),(1,1),(0,1). Orient the path so its direction is out of the paper by the right hand rule
- - a) 3.43E-01
- - b) 3.67E-01
- - c) 3.93E-01
- - d) 4.21E-01
- + e) 4.50E-01
5. What is the magnitude of the electric field at the origin if a 3.1 nC charge is placed at x = 6.2 m, and a 2.6 nC charge is placed at y = 6 m?
- -a) 5.47 x 10-1N/C
- -b) 6.32 x 10-1N/C
- -c) 7.3 x 10-1N/C
- -d) 8.43 x 10-1N/C
- +e) 9.73 x 10-1N/C
6. What angle does the electric field at the origin make with the x-axis if a 2 nC charge is placed at x = -8 m, and a 1.4 nC charge is placed at y = -9.3 m?
- -a) 2.37 x 101degrees
- +b) 2.74 x 101degrees
- -c) 3.16 x 101degrees
- -d) 3.65 x 101degrees
- -e) 4.22 x 101degrees
7. A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the x component of the electric field at (x,y) =( 4a, 2a) is βkQ/a2, where β equals
- -a) 7.31 x 10-3 unit
- -b) 8.86 x 10-3 unit
- -c) 1.07 x 10-2 unit
- -d) 1.3 x 10-2 unit
- +e) 1.57 x 10-2 unit
8. A dipole at the origin consists of charge Q placed at x = 0.5a, and charge of -Q placed at x = -0.5a. The absolute value of the y component of the electric field at (x,y) =( 1.1a, 1.2a) is βkQ/a2, where β equals
- -a) 2.36 x 10-1 unit
- -b) 2.86 x 10-1 unit
- +c) 3.47 x 10-1 unit
- -d) 4.2 x 10-1 unit
- -e) 5.09 x 10-1 unit
9. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 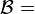
- - a) −7
- - b) 3
- - c) −3
- - d) −3
- + e) 2
10. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 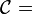 :
:
- - a) s−4
- - b) 5−s
- + c) 1−s
- - d) s−1
- - e) 5
11. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the y component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 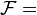 :
:
- + a) 3/2
- - b) 1/2
- - c) 3
- - d) 2
- - e) 2/3
12. A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 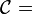 :
:
- - a) s−7
- - b) 8
- - c) 3−s
- + d) 7−s
- - e) s−3
13. A line of charge density λ situated on the x axis extends from x = 3 to x = 7. What is the x component of the electric field at the point (7, 8)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 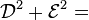 :
:
- - a) 32 + 82
- + b) (7-s)2 + 82
- - c) 72 + (8−s)2
- - d) 72 + (3−s)2
- - e) 72 + 82
14. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 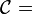
- - a) s−7
- - b) s−3
- - c) 3
- + d) 7−s
- - e) 3−s
15. A line of charge density λ situated on the y axis extends from y = -3 to y = 2. What is the y component of the electric field at the point (3, 7)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where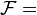
- - a) 2
- - b) 1/2
- + c) 3/2
- - d) 3
16. A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
 (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 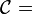 :
:
- - a) s − 9
- - b) 2
- + c) 9 − s
- - d) 2 − s
- - e) s − 2
17. A line of charge density λ situated on the y axis extends from y = 2 to y = 7. What is the y component of the electric field at the point (2, 9)?
 (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 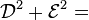 :
:
- - a) 92 + (2-s)2
- - b) 92 + (7-s)2
- - c) 72 + (2-s)2
- + d) 22 + (9-s)2
- - e) 22 + (7-s)2
18. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 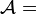 :
:
- - a) 1/2
- - b) 2
- - c) 8
- + d) 4
19. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the y component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 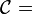 :
:
- + a) 4
- - b) s−4
- - c) 8−s
- - d) 4−s
- - e) s−8
20. A line of charge density λ situated on the x axis extends from x = 4 to x = 8. What is the x component of the electric field at the point (8, 4)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 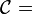 :
:
- - a) s−4
- + b) 8−s
- - c) s−8
- - d) 4
- - e) 4−s
21. A line of charge density λ situated on the y axis extends from y = 4 to y = 6. What is the x component of the electric field at the point (5, 1)? (assuming
(assuming  )
) ![is: \frac{1}{4\pi\epsilon_0}\int_\mathcal A^\mathcal B\frac{ \mathcal C\;\lambda ds}{\left[\mathcal D^2+\mathcal E^2\right]^\mathcal F\;}](../I/m/d67cf607bcd5329c89d44f432d252ea0.png) , where
, where 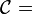 :
:
- - a) s−4
- - b) s−1
- - c) 1−s
- - d) 5−s
- + e) 5
22. A cylinder of radius, R, and height H has a uniform charge density of 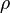 . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
. The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z > H/2?
- - a)c)
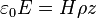
- - a)c)
- - b)d) none of these are correct
- + c)e)
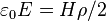
- + c)e)
- - d)
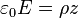
- - d)
- - e)b)
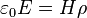
- - e)b)
23. A cylinder of radius, R, and height H has a uniform charge density of 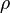 . The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
. The height is much less than the radius: H << R. The electric field at the center vanishes. What formula describes the electric field at a distance, z, on axis from the center if z < H/2?
- - a)b) none of these are correct
- - b)e)
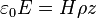
- - b)e)
- - c)d)
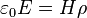
- - c)d)
- + d)c)
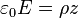
- + d)c)
- - e)
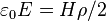
- - e)
24. A sphere has a uniform charge density of 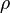 , and a radius or R. What formula describes the electric field at a distance r > R?
, and a radius or R. What formula describes the electric field at a distance r > R?
- - a) none of these are correct
- - b)d)
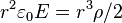
- - b)d)
- + c)e)

- + c)e)
- - d)c)
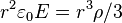
- - d)c)
- - e)b)

- - e)b)
25. A sphere has a uniform charge density of 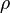 , and a radius equal to R. What formula describes the electric field at a distance r < R?
, and a radius equal to R. What formula describes the electric field at a distance r < R?
- - a)
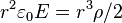
- - a)
- - b)b)

- - b)b)
- + c)d)
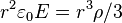
- + c)d)
- - d)c) none of these are correct
- - e)e)

- - e)e)
26. A cylinder of radius, R, and height H has a uniform charge density of 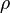 . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
. The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r < R?
- - a)b)
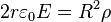
- - a)b)
- - b)d) none of these are correct
- - c)
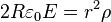
- - c)
- + d)c)
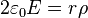
- + d)c)
- - e)e)
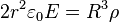
- - e)e)
27. A cylinder of radius, R, and height H has a uniform charge density of 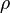 . The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
. The height is much greater than the radius: H >> R. The electric field at the center vanishes. What formula describes the electric field at a distance, r, radially from the center if r > R?
- - a)
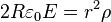
- - a)
- - b)b)
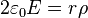
- - b)b)
- + c)c)
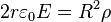
- + c)c)
- - d)e)
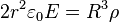
- - d)e)
- - e)d) none of these are correct
- Attribution (for quiz questions) under CC-by-SA license
- http://en.wikiversity.org/w/index.php?title=Quizbank/College_Physics/a07energy_lineIntegral&oldid=1381800
- http://en.wikiversity.org/w/index.php?title=Physics_equations/18-Electric_charge_and_field/Q:findE&oldid=1378605
- http://en.wikiversity.org/w/index.php?title=Physics_equations/18-Electric_charge_and_field/Q:lineChargesCALCULUS&oldid=1390982
- http://en.wikiversity.org/w/index.php?title=Physics_equations/19-Electric_Potential_and_Electric_Field/Q:UsingGaussLaw&oldid=1391093
- Study guide
- http://en.wikiversity.org/wiki/Physics_equations/Sheet/All_chapters
- http://en.wikiversity.org/w/index.php?title=Physics_equations/Sheet/All_chapters&oldid=1283423