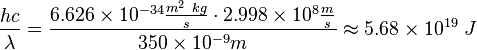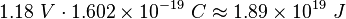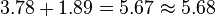Quantum mechanics/Photoelectric effect/Lab

< Quantum mechanics < Photoelectric effect

This lab uses http://phet.colorado.edu/en/simulation/photoelectric

This lab is historically important because it represents the second appearance of a successful physics model that involves Plank's constant. And with almost any successful model that involves Plank's constant, it permits one to calculate the numerical value of the constant. It is only the fact that all such models yield consistent numerical values that allow us to view Plank's constant as a "universal" constant of nature.

Open and run http://phet.colorado.edu/en/simulation/photoelectric'''. You should see electrons being emitted from the cathode. If these electrons strike the anode, a current, I, will be measured. You can adjust the voltage, V, using the button on what looks like a battery.

Measuring the cutoff voltage

Our first task is to measure the cutoff voltage associated with the photoelectric effect. Begin with a single configuration that you should document:

Pick a metal
Pick a wavelength.
Set the intensity to the maximum amount.

All metals need to investigated by the entire class, but if the class is small, this lab can be performed using only one metal. There are three ways to measure the cutoff voltage:

Adjust the voltage until the current just barely stops.
Measure two values of (I,V) near zero and find the straight line that passes through them. The cutoff voltage is where the line passes through the V axis. This can be done using algebra (by hand).
OPTIONAL: Measure three or more values of (I,V) and use a data-analysis procedure to fit it to a curve. This requires a computer and picking the right curve can be tricky (of even treacherous). See if your data is subject to the problem of overfitting.

Calculating the formula

While a simple formula describes the photoelectric effect, it is a tricky formula to use because the units are somewhat exotic. For most people, it is simplest to first convert everything into SI (mks) units: Wavelength is measured in meters, frequency in Hz (inverse seconds), energy is measured in Joules (not eV as is typical in some contexts -- 1ev=1.602x10^-19J where J is the symbol for Joules'.

Two important derived SI units are the Volt and the Coulomb.

The work Function is the difference in an electron's potential energy at the surface of a metal. Measured in Joules, it is the work required to bring an electron from rest inside the metal, to a position at rest just outside the surface of the metal.
Another potential energy barrier for the electrons is supplied by the power supply, and measured as the "voltage" in the simulation. This potential energy is qV, where q is the charge of the electron q=1.602x10^-19C) where C is the symbol for Coulombs, an SI unit.

Sample calculation

Using the simulator, it was found with Sodium that λ=350nm, and V_cut=1.18V. The work function of sodium (Na) is 2.36 eV.

The energy delivered by the photon to the electron residing in the metal is

\frac{hc}{\lambda} = \frac{ 6.626\times 10^{-34}\frac{m^2 \ kg}{s} \cdot 2.998\times 10^8 \frac{m}{s} }{350\times 10^{-9}m}\approx 5.68\times 10^{19} \ J

The energy associated with the work function is the energy required to move the electron from inside the metal to just outside its surface, is

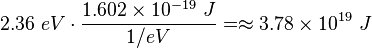2.36 \ eV \cdot \frac{1.602\times 10^{-19} \ J}{ 1 / eV}= \approx 3.78\times 10^{19} \ J

The energy lost by a free electron as it transits the applied voltage drop between the cathode and the anode is

1.18 \ V\cdot 1.602\times 10^{-19} \ C \approx 1.89\times 10^{19} \ J

Note that

3.78+1.89=5.67\approx 5.68

This article is issued from Wikiversity - version of the Saturday, September 20, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.